27. Каноническое уравнение прямой. Параметрическое уравнение прямой
Пусть дана прямая 
. Направляющий вектор произвольной прямой обозначим 
, а его координаты 
и имеющей данный направляющий вектор 
. Пусть 
- произвольная точка прямой (рис.25). Возьмем вектор
,
являющийся коллинеарным направляющему вектору . Следовательно, координаты вектора 
пропорциональны координатам вектора :
(1)
Мы получили уравнение прямой, проходящей через точку в направлении . Уравнение (1) называется Каноническим уравнением прямой.
Обозначим буквой 
каждое из равных отношений выражения (1)
(2)
Из равенств (2) следует
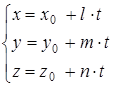(3)
Уравнение (3) называется параметрическим уравнением прямой. В этом уравнении рассматривается как произвольно изменяющийся параметр, 
- как функции от ; при изменении величины меняются так, что точка движется по данной прямой.
Пример 1. Привести к каноническому виду уравнения прямой
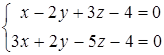
Решение. Определим координаты какой-либо точки на прямой. Для этого положим в обоих уравнениях 
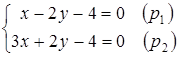(1)
Найдем 
. Таким образом, точка 
принадлежит данной прямой (1).
Направляющий вектор найдем как векторное произведение нормалей к данным плоскостям 
и 
, где 
и 
. Получим
.
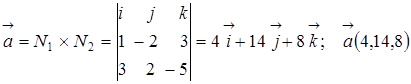Имея точку 
, принадлежащую прямой, и ее направляющий вектор , можем написать каноническое уравнение данной прямой
или 
Пример 2. Написать каноническое и параметрическое уравнение прямой, проходящей через точку 
параллельно оси 
.
Решение. По условию вектор 
, расположенный на оси , параллелен искомой прямой, поэтому его можно считать направляющим вектором этой прямой. Запишем уравнение прямой
| < Предыдущая | Следующая > |
|---|
