26. Прямая линия
Всякая прямая линия 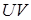 может быть задана системой двух уравнений плоскостей
может быть задана системой двух уравнений плоскостей  , проходящих через прямую
, проходящих через прямую 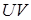 . Всякая точка
. Всякая точка 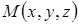 , лежащая на прямой
, лежащая на прямой 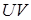 , Принадлежит обеим плоскостям
, Принадлежит обеим плоскостям  и
и 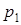 и, значит, координаты
и, значит, координаты 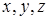 удовлетворяют обоим уравнениям (1) и (2):
удовлетворяют обоим уравнениям (1) и (2):
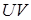 , заданной уравнениями (1), (2) можно принять векторное произведение
, заданной уравнениями (1), (2) можно принять векторное произведение 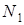 и
и 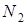 нормальных векторов к плоскостям
нормальных векторов к плоскостям 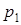 и
и 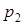 . Так как
. Так как 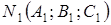 , а
, а 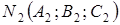 , то
, то

Лежащий на прямой ![]() (или параллельный ей) ненулевой вектор называется Направляющим вектором. Координаты
(или параллельный ей) ненулевой вектор называется Направляющим вектором. Координаты ![]() направляющего вектора называются Направляющими коэффициентами прямой
направляющего вектора называются Направляющими коэффициентами прямой ![]() .
.
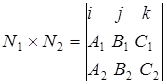
Или
 (3)
(3)
| < Предыдущая | Следующая > |
|---|