24. Расстояние от точки до плоскости

Найдем расстояние От данной точки до данной плоскости

. (1)

Искомое расстояние мы найдем по формуле

(2)

Где - координаты основания перпендикуляра, опущенного из точки на плоскость (1). Найдем координаты .

Во-первых, они удовлетворяют уравнению (1), т. к. точка лежит на этой плоскости:

(3)

Во-вторых, вектор по построению перпендикулярен к плоскости (1) и, значит, коллинеарен с нормальным вектором плоскости (1). Следовательно, их соответственные координаты пропорциональны

(4)

Выразим из (4) через

(5)

Перепишем равенства (5) в виде

(6)

Подставим эти выражения в (3). Получим

(7)

Преобразуем его относительно , будем иметь

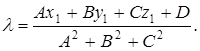(8)

Подставим выражения (5) в (2)

(9)

Далее в (9) подставим выражение (8), получим

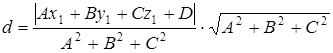
Или

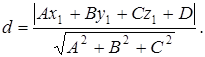(10)

Следовательно, чтобы найти расстояние от данной точки до данной плоскости (1), достаточно подставить в левую часть уравнения (1) координаты данной точки , результат разделить на квадратный корень из суммы квадратов коэффициентов уравнения (1) при текущих координатах и взять абсолютную величину частного.

< Предыдущая		Следующая >