23. Взаимное расположение прямых и плоскостей

Рассмотрим случаи взаимного расположения плоскостей

(1)

(2)

Случай 1. Плоскости и параллельны или не параллельны, смотря по тому, коллинеарны или неколлинеарны их нормальные векторы

(3)

Поэтому, если плоскости (1) и (2) параллельны, то их нормальные векторы коллинеарны и для них выполняется условие

(4)

Где - коэффициент пропорциональности.

Условием совпадения плоскостей (1) и (2) является пропорциональность всех коэффициентов, включая свободные члены

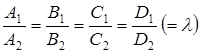. (5)

Случай 2. Плоскости (1) и (2) перпендикулярны или не перпендикулярны, смотря по тому, перпендикулярны или нет их нормальные векторы и

Поэтому, если плоскости (1) и (2) перпендикулярны, то их нормальные векторы перпендикулярны, а, следовательно, их скалярное произведение равно нулю

. (6)

Случай 3. Если плоскости (1) и (2) пересекаются, образуя четыре двухгранных угла, равных попарно. Когда говорят «угол между плоскостями» (1) и (2), то имеют в виду любой из этих углов и приписывают ему значение , заключенное между и . Одно из значений равняется углу между нормальными векторами и другое дополняет первое до .

Применяя формулу для вычисления угла между векторами, получим

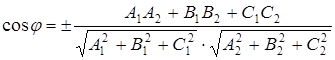. (7)

< Предыдущая		Следующая >