22. Уравнение плоскости, проходящей через три точки

Решим в общем виде задачу, в которой нужно составить уравнение плоскости, проходящей через три различные точки:

.

Обозначим через координаты произвольной точки пространства и рассмотрим три вектора:

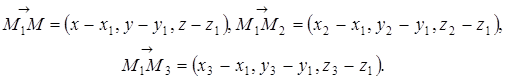
Точка Лежит на плоскости в том и только в том случае, когда векторы И компланарны. Условием компланарности этих трех векторов является равенство нулю определителя третьего порядка, составленного из их координат.

В данном случае имеем:

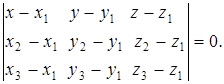(1)

Это и есть искомое уравнение плоскости, проходящей через три точки и .

< Предыдущая		Следующая >