2. Преобразование прямоугольной системы координат

При решении задач иногда выгодно, вместо данной прямоугольной системы координат , выбрать другую прямоугольную систему координат , определенным образом ориентированную относительно первой.

Рассмотрим сначала простейший случай (см. рис.1), когда оси «новой системы координат» параллельны соответствующим осям « старой системы координат» и имеют одинаковые направления с ними (параллельный перенос системы координат).

Пусть начало новой системы координат имеет коорди­наты в старой системе координат. Точка плоско­сти со «старыми координа­тами» будет иметь неко­торые «новые координаты» . Из рис.1 получаем

Рис.1

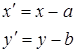, (1) то есть новые координаты точки равны ее старым координатам минус старые координаты нового начала.

Обратно из (1) находим

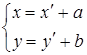(2)

Рис.2

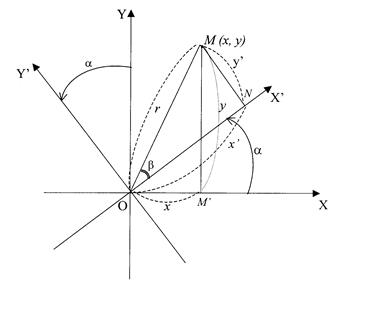Пусть теперь «новая система» координат , при неизменном начале , повернута относительно старой системы на угол , т. е. , причем угол считается положительным, если поворот осуществляется против часовой стрелки и отрицательным – в противоположном случае (рис.2).

Обозначим через угол, образованный радиусом-вектором точки с осью ; тогда отрезок , с учетом знака , будет составлять с осью угол . Отсюда на основании формул при любом расположении точки имеем:

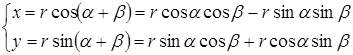(3)

Так как новые координаты точки есть

, (4)

То из формул (3) получаем

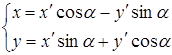(5)

Формулы (5) выражают старые координаты и точки через ее новые координаты и . Чтобы выразить новые координаты и через старые и , достаточно разрешить систему (5) относительно и . Но можно поступить проще: а именно, принять систему за «старую», а систему XOY за «новую». Тогда, учитывая, что вторая система повернута относительно первой на угол , заменяя в формулах (5) и Соответственно на и , и обратно принимая во внимание, что , будем иметь

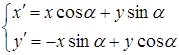
(6)

Наконец, в общем случае, когда новое начало координат есть точка и ось образует с осью угол , соединяя формулы (2) и (5), находим

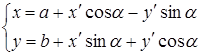(7)

Аналогично, из формул (1) и (6) получим

(8)

< Предыдущая		Следующая >