19. Общее уравнение плоскости

Плоскость 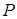в пространстве можно задать некоторой ее точкой 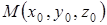и ненулевым вектором , перпенди­кулярным этой плоскости (нормальный или направляющий вектор плоскости).

Пусть - радиус-вектор точки , а - радиус-вектор произвольной точки Плоскости (рис.22). Тогда вектор расположен в данной плоскости и, следовательно, ортогонален вектору , т. е. . Используя условие ортогональности двух векторов, имеем

(1)

Это и есть уравнение плоскости в векторном виде. В координатной форме уравнение (1) имеет вид:

(2)

Или

(3)

Где .

Уравнение (3) называется Общим уравнением плоскости первой степени относительно текущих координат

Таким образом плоскость есть поверхность первого порядка. Уравнение (2) задает плоскость, проходящую через точку , перпендикулярно вектору .

< Предыдущая		Следующая >