18. Полярные координаты. Параметрические уравнения линии

Наиболее важной после прямоугольной системы является полярная система координат.

Рис.18

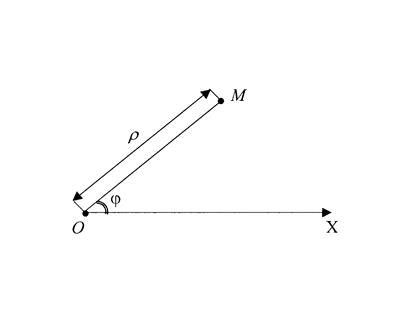Возьмем на плоскости точку , которая называется полюсом. Проведем из полюса направленную полупрямую , называемую полярной осью (рис.18). Пусть - произвольная точка плоскости. Соединим точку С полюсом Отрезком . Длина отрезка , т. е. расстояние точки от полюса, называется Полярным радиусом точки , а угол , отсчитываемый от полярной оси к отрезку Против движения часовой стрелки, Полярным углом.

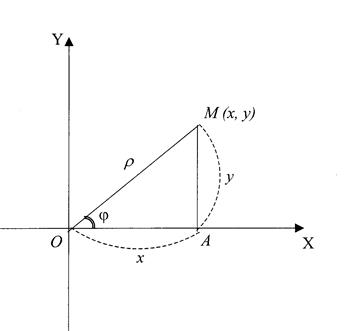Полярный радиус и полярный угол и Составляют Полярные координаты точки , и записывается следующим образом .

Рассмотрим переход от полярных координат к прямоугольным и обратно.

Рис.19

Пусть полюс полярной системы совпадает в началом прямоуголь­ной системы координат , а по­лярная ось является положительной полуосью (рис.19). Тогда для произвольной точки имеем:

Считая угол острым, из прямоугольного находим

Или

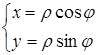
Полученные формулы справедливы для любого угла и выражают прямоугольные координаты точки через ее полярные координаты.

Выразим полярные координаты точки через прямоугольные координаты из того же прямоугольника

Или

Пример 1. Найти полярное уравнение прямой

Решение. Так как , то или . Это и есть уравнение данной прямой в полярных координатах.

Пример 2. Написать уравнение линии в полярных координатах.

Решение. Так как , а Подставим эти выражения в данное уравнение линии

или

Это уравнение данной линии в полярных координатах.

Иногда бывает удобнее вместо уравнения линии в прямоугольных координатах, рассматривать параметрические уравнения линии, дающие выражения текущих координат и в виде функций от некоторой переменной величины (параметра).

Пример 1. Выведем параметрическое уравнение окружности.

Решение. Пусть - произвольная точка окружности радиуса с центром в начале координат (рис.20). В прямоугольном треугольнике обозначим угол через . Будем иметь равенства

Рис.20

Или

Рис.20

(1)

Это и есть параметрическое урав­нение окружности.

Пример 2. Параметрическое уравнение эллиса.

Решение. Эллипс с полуосями и можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса , где коэффициент сжатия . Пусть - точка эллипса и - соответствующая точка окружности (рис.21), где

Рис.21

. (1)

За параметр Примем угол, образованный радиусом окружности с положительным направлением оси : Используя формулы (1) имеем

Таким образом, параметрические уравнения эллипса с полуосями и есть

. (2)

< Предыдущая		Следующая >