17. Нецентральные кривые второго порядка
Кривая второго порядка называется нецентральной, если она или не имеет центра симметрии, или же имеет бесконечно много центров симметрии.
Рассмотрим кривую второго порядка
![]() (1)
(1)
Где ![]() и
и ![]() . Для определенности будем считать, что
. Для определенности будем считать, что
![]() ,
, ![]() (2)
(2)
Кроме того, предположим, что ![]() , в противном случае мы бы имели пару параллельных прямых.
, в противном случае мы бы имели пару параллельных прямых.
Дополняя в уравнении (1) члены с ![]() до полного квадрата, будем иметь
до полного квадрата, будем иметь

Или, полагая
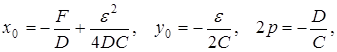 (3)
(3)
Получим

![]() . (4)
. (4)
|
Кривая (4) называется Параболой (рис.16); точка
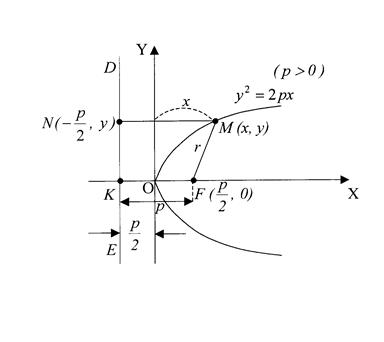
![]() (5)
(5)
Если поменять местами оси ![]() и
и ![]() , то каноническое уравнение параболы примет вид
, то каноническое уравнение параболы примет вид
![]() (6)
(6)
Это уравнение параболы с вертикальной осью (рис.17 а)).
|

![]()
|
|
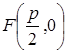 называется ее Фокусом, а прямая
называется ее Фокусом, а прямая  (7)
(7)
С другой стороны расстояние этой точки до директрисы равно
![]()
Таким образом, парабола представляет собой множество всех точек плоскости, равноотстоящих от данной точки (фокуса) и от данной прямой (директрисы).
Пример 1. Составить каноническое уравнение эллипса, зная, что его большая полуось ![]() , а эксцентриситет
, а эксцентриситет ![]() Найти расстояние между фокусами эллипса.
Найти расстояние между фокусами эллипса.
Решение. Воспользуемся формулой, выражащающей эксцентриситет через отношение полуосей:
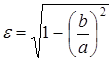 или
или 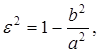
Откуда ![]()
В данном случае ![]()
Следовательно, каноническое уравнение эллипса
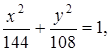
Так как ![]() , то
, то ![]() ;
; ![]() и расстояние между фокусами
и расстояние между фокусами ![]()
Пример 2. Асимптоты гиперболы имеют уравнения ![]() а расстояние между фокусами равно
а расстояние между фокусами равно ![]() . Написать ее каноническое уравнение.
. Написать ее каноническое уравнение.
Решение. Разрешим уравнение асимптот относительно ![]() И, сравнив с общей формулой асимптот, найдем отношение
И, сравнив с общей формулой асимптот, найдем отношение ![]() к
к ![]() :
:
![]()
Кроме того, ![]() т. е.
т. е. ![]() Так как для гиперболы
Так как для гиперболы ![]() то для нахождения
то для нахождения ![]() и
и ![]() получим систему уравнений
получим систему уравнений

Решая систему найдем ![]() . Следовательно, каноническое уравнение гиперболы имеет вид
. Следовательно, каноническое уравнение гиперболы имеет вид
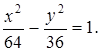
Пример 3. Парабола с вершиной в начале координат проходит через точку ![]() и симметрична относительно оси
и симметрична относительно оси ![]() . Написать ее уравнение.
. Написать ее уравнение.
Решение. Так как парабола симметрична относительно оси ![]() и проходит через точку A c положительной абсциссой, то она имеет вид
и проходит через точку A c положительной абсциссой, то она имеет вид ![]() . Подставляя координаты точки
. Подставляя координаты точки ![]() в уравнение такой параболы, получим
в уравнение такой параболы, получим ![]() , т. е.
, т. е. ![]()
Следовательно, искомое уравнение ![]() , фокус этой параболы
, фокус этой параболы ![]() , уравнение директрисы
, уравнение директрисы ![]()
| < Предыдущая | Следующая > |
|---|