16. Фокальные свойства центральных кривых второго порядка

Точки и , где

, (1)

Называются Фокусами, соответственно эллипса, заданного каноническим уравнением (8) (рис.14) (знак - ) и гиперболы, заданной каноническим уравнением (11) (рис.15; знак + ).

Отношение

(2)

Называется Эксцентриситетом центральной кривой второго порядка.

Из формулы (1) имеем: для эллипса , для гиперболы . Для окружности .

Пусть и - расстояния точки Центральной кривой второго порядка от ее фокусов ( называемые фокальными радиусами точки .

Имеем

(3)

И

. (4)

Так как 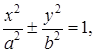где знак плюс соответствует эллипсу, знак минус – гиперболе, то

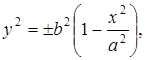
И, следовательно, с учетом (1), получаем

(5)

И, аналогично,

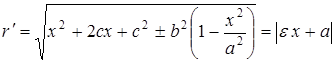. (6)

Если кривая – эллипс, то , и поэтому

Отсюда

(7)

Причем для любых и , удовлетворяющих равенству (7), существует точка данного эллипса. Таким образом, для любой точки эллипса сумма ее фокальных радиусов есть величина постоянная. Это свойство принимается за определение эллипса.

Для гиперболы имеем: , , поэтому

,

Где знак (+) соответствует правой ветви гиперболы , знак (-) соответствует левой ветви . Отсюда

(8)

Таким образом для любой точки гиперболы абсолютная величина разности ее фокальных радиусов есть величина постоянная.

4. Асимптоты гиперболы

Рассмотрим гиперболу (рис.15)

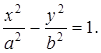(1)

Решая уравнение (1) относительно , получаем

(2)

Или

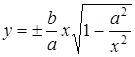. (3)

Если неограниченно возрастает, то 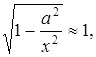и, следовательно, имеет место приближенное равенство

Ветви гиперболы (1) сколь угодно близко приближаются к прямым

(4)

Которые называются Асимптотами гиперболы.

< Предыдущая		Следующая >