15. Центральные кривые второго порядка
Рассмотрим уравнение кривой второго порядка ![]() (1)
(1)
![]() без члена с произведением координат
без члена с произведением координат ![]() и
и ![]()
![]() .
.
Дополним члены, содержащие ![]() и
и ![]() До полных квадратов. Будем иметь
До полных квадратов. Будем иметь
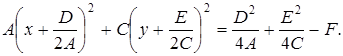 (2)
(2)
Полагая
![]() (3)
(3)
И
 , (4)
, (4)
Получаем
![]() . (5)
. (5)
Точка ![]() есть центр симметрии кривой (5). Параллельные осям координат
есть центр симметрии кривой (5). Параллельные осям координат ![]() И
И ![]() прямые
прямые ![]() являются осями симметрии кривой (5).
являются осями симметрии кривой (5).
Действительно, если точка ![]() лежит на кривой (5), то симметричная ей относительно прямой
лежит на кривой (5), то симметричная ей относительно прямой ![]() точка
точка ![]() также лежит на этой кривой. Аналогичным свойством обладает прямая
также лежит на этой кривой. Аналогичным свойством обладает прямая ![]() .
.
В дальнейшем будем предполагать, что центр кривой находится в начале координат, т. е. ![]() . Тогда уравнение кривой примет вид
. Тогда уравнение кривой примет вид
![]() . (6)
. (6)
Определение 1. Кривая второго порядка (6) называется эллипсом (т. е. принадлежит эллиптическому типу), если коэффициенты А и С имеют одинаковые знаки, т. е.
![]() . (7)
. (7)
Будем предполагать, что ![]() и
и ![]() . Возможны три случая:1)
. Возможны три случая:1) ![]() , 2)
, 2) ![]() и 3)
и 3) ![]() .
.
В первом случае, ![]() имеем действительный эллипс
имеем действительный эллипс
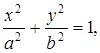 (8)
(8)
Где числа
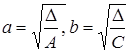 , (9)
, (9) 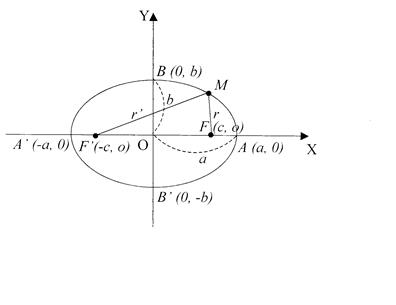 Называются полуосями эллипса.
Называются полуосями эллипса.
|
Отметим, что из уравнения (8) имеем ![]() При
При ![]() получаем Окружность
получаем Окружность
![]() .
.
Во втором случае, ![]() , кривая (6) представляет собой точку
, кривая (6) представляет собой точку ![]() (вырожденный эллипс).
(вырожденный эллипс).
В третьем случае, ![]() , кривая (6) не имеет действительных точек; ее условно называют мнимым эллипсом.
, кривая (6) не имеет действительных точек; ее условно называют мнимым эллипсом.
Определение 2. Кривая второго порядка называется Гиперболой (т. е. кривой гиперболического типа), если коэффициенты ![]() и
и ![]() имеют противоположные знаки, т. е.
имеют противоположные знаки, т. е.
![]() . (10)
. (10)
Пусть ![]() , а
, а ![]() . Рассмотрим три случая: 1)
. Рассмотрим три случая: 1) ![]() , 2)
, 2) ![]() и
и
3) ![]() .
.
В первом случае, ![]() , имеем гиперболу с каноническим уравнением
, имеем гиперболу с каноническим уравнением
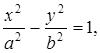 (11)
(11)
 Где
Где 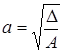 (действительная полуось) и
(действительная полуось) и 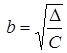 (мнимая полуось) (рис.15). Точки
(мнимая полуось) (рис.15). Точки ![]() - называются вершинами гиперболы, где
- называются вершинами гиперболы, где ![]()
Во втором случае, ![]() , получаем пару пересекающихся прямых (вырожденная гипербола)
, получаем пару пересекающихся прямых (вырожденная гипербола) ![]()
В третьем случае, ![]() , получим гиперболу
, получим гиперболу
|
 (12)
(12)
С полуосями 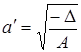 и
и 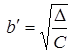 . Если
. Если ![]() и
и ![]() , то гипербола (12) называется Сопряженной к гиперболе (11); ее вершины
, то гипербола (12) называется Сопряженной к гиперболе (11); ее вершины ![]() (рис.15).
(рис.15).
Отрезок ![]() называется действительной осью, а отрезок
называется действительной осью, а отрезок ![]() - мнимой осью гиперболы (11).
- мнимой осью гиперболы (11).
Пример. Определить вид и расположение кривой ![]()
Решение. Дополняя члены, содержащие ![]() и
и ![]() , соответственно, до полных
, соответственно, до полных 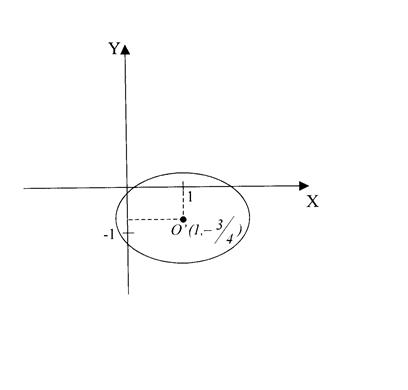 Квадратов, будем иметь
Квадратов, будем иметь
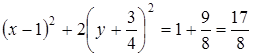 .
.
Приведем к каноническому виду
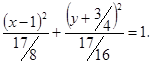
Следовательно, данная кривая есть эллипс с полуосями ![]() , центр которого находится в точке
, центр которого находится в точке 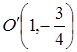 .
.
| < Предыдущая | Следующая > |
|---|