14. Окружность
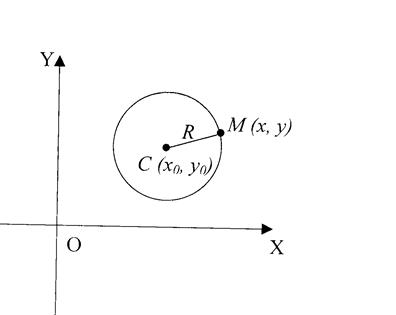 Выведем уравнение окружности (рис.13) с центром в точке
Выведем уравнение окружности (рис.13) с центром в точке ![]() и радиусом
и радиусом ![]() . Для произвольной точки
. Для произвольной точки ![]() окружности выполнено равенство
окружности выполнено равенство
![]() . (1)
. (1)
По формуле расстояния между двумя точками имеем
![]() . (2)
. (2)
Так как обе части равенства (2) положительны, то, возводя в квадрат, получим равносильное уравнение
![]() . (3)
. (3)
Координаты любой точки ![]() данной окружности удовлетворяют уравнению (3). Таким образом, уравнение (3) представляет собой уравнение окружности радиуса
данной окружности удовлетворяют уравнению (3). Таким образом, уравнение (3) представляет собой уравнение окружности радиуса ![]() с центром в точке
с центром в точке ![]() . Это уравнение называется нормальным уравнением окружности.
. Это уравнение называется нормальным уравнением окружности.
В частности, полагая ![]() и
и ![]() , получим уравнение окружности с центром в начале координат
, получим уравнение окружности с центром в начале координат
![]() . (4)
. (4)
Уравнение (3) можно привести к виду
![]() (5)
(5)
Где ![]()
Таким образом окружность является кривой второго порядка. Сравнивая уравнение (5) с общим уравнением кривой второго порядка
![]() (6)
(6)
Видим, что в (5) ![]() и
и ![]() , т. е.
, т. е. ![]()
Обратно, положим в (6) ![]() и
и ![]() :
:
![]() . (7)
. (7)
Деля уравнение (7) почленно на ![]() и полагая
и полагая
![]() , (8)
, (8)
Получим уравнение вида (5).
Уравнение (7) называется общим уравнением действительной окружности при  , где
, где ![]() выражаются равенствами (8).
выражаются равенствами (8).
Таким образом: действительная кривая второго порядка является окружностью тогда и только тогда, когда
1) коэффициенты при квадратах текущих координат равны между собой и
2) отсутствует член, содержащий произведение текущих координат.
| < Предыдущая | Следующая > |
|---|