13. Расстояние точки до прямой
Рассмотрим кривую ![]() , заданную общим уравнением
, заданную общим уравнением

![]() (1)
(1)
|
![]()
Так как ![]() , то
, то 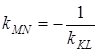 , а
, а ![]() . Следовательно, уравнение перпендикуляра
. Следовательно, уравнение перпендикуляра ![]() имеет вид
имеет вид
![]() или
или ![]() . (2)
. (2)
Основание перпендикуляра ![]() удовлетворяет его уравнению (2); будем иметь
удовлетворяет его уравнению (2); будем иметь
![]() (3)
(3)
И, следовательно,
![]() (4)
(4)
Где ![]() - коэффициент пропорциональности.
- коэффициент пропорциональности.
Поэтому
![]() . (5)
. (5)
С другой стороны, учитывая, что точка ![]() лежит на прямой
лежит на прямой ![]() , из (4) имеем
, из (4) имеем
![]()
Получаем
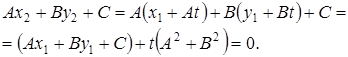
Следовательно,
![]() (6)
(6)
Таким образом, в силу формулы (5) имеем
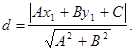 (7)
(7)
Разделив обе части уравнения (1) на ![]() , получим уравнение
, получим уравнение
![]() (8)
(8)
Такое уравнение прямой называется Нормированным.
Из формулы (7) получаем правило: чтобы определить расстояние точки от прямой, нужно в левую часть нормированного уравнения этой прямой подставить координаты данной точки и взять абсолютное значение полученного результата.
Пример 1. Найти точку ![]() , симметричную точке
, симметричную точке ![]() относительно прямой
относительно прямой ![]()
Решение. Симметричные точки ![]() и
и ![]() расположены на одном перпендикуляре к данной прямой на одинаковом расстоянии от нее. Угловой коэффициент данной прямой
расположены на одном перпендикуляре к данной прямой на одинаковом расстоянии от нее. Угловой коэффициент данной прямой ![]() . Угловой коэффициент перпендикулярной к ней прямой
. Угловой коэффициент перпендикулярной к ней прямой 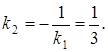 Уравнение перпендикуляра найдем по формуле
Уравнение перпендикуляра найдем по формуле
![]() или
или ![]() .
.
Найдем теперь точку пересечения данной прямой с перпендикулярной, решая их уравнения:
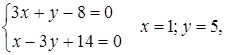 точка
точка ![]() .
.
Так как точка С является серединой отрезка ![]() , то, зная точки
, то, зная точки ![]() и
и ![]() , находим координаты искомой точки
, находим координаты искомой точки ![]() :
:
![]()
Таким образом, искомая точка имеет координаты ![]() .
.
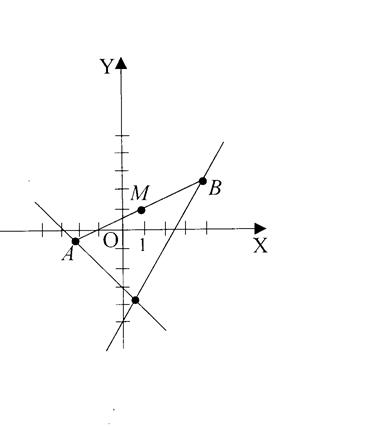
Пример 2. Найти прямую, пересекающую прямые ![]() и
и ![]() в точках
в точках ![]() и
и ![]() так, что серединой отрезка
так, что серединой отрезка ![]() является данная точка
является данная точка ![]() (см. рис.).
(см. рис.).
Решение. Искомая прямая проходит через точку ![]() , поэтому ее уравнение запишем в виде
, поэтому ее уравнение запишем в виде
![]() или
или ![]() .
.
Для нахождения ![]() используем то условие, что точка
используем то условие, что точка ![]() Делит отрезок
Делит отрезок ![]() пополам. Так как искомая прямая пресекает данные в точках
пополам. Так как искомая прямая пресекает данные в точках ![]() и
и ![]() , то их координаты будут найдены из следующих систем уравнений:
, то их координаты будут найдены из следующих систем уравнений:
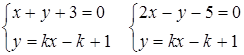 .
.
Но поскольку ![]() неизвестно, то из этих систем координаты точек
неизвестно, то из этих систем координаты точек ![]() и
и ![]() выразятся через
выразятся через ![]() . Достаточно выразить через
. Достаточно выразить через ![]() абсциссы
абсциссы ![]() И
И ![]() Точек
Точек ![]() и
и ![]() . Для этого, исключая из каждой системы
. Для этого, исключая из каждой системы ![]() , получим
, получим
![]() и
и ![]() .
.
По формуле деления отрезка пополам полусумма этих значений абсцисс должна давать абсциссу середины отрезка, т. е.
 откуда
откуда ![]() .
.
Таким образом, искомая прямая имеет уравнение
![]()
| < Предыдущая | Следующая > |
|---|