12. Точка пересечения двух прямых

Пусть имеем две прямые

(1)

. (2)

Точка пересечения этих прямых лежит как на первой, так и на второй. Поэтому координаты точки пересечения должны удовлетворять обоим уравнениям (1) и (2). Следовательно, для того чтобы найти координаты точки пересечения двух данных прямых необходимо решить совместно систему уравнений этих прямых: .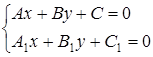

Последовательно исключая и уравнений системы неизвестные и , будем иметь

.

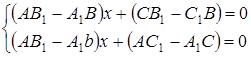Отсюда, если , то для координат точки пересечения прямых получаем выражения

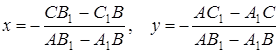(3)

Или, введя определители второго порядка, имеем

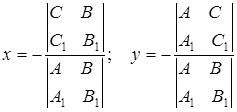. (4)

Для прямых (1) и (2) возможны следующие три случая.

1) , т. е. в этом случае прямые не параллельны.

2) , или , т. е. .

В этом случае прямые (1) и (2) сливаются, и таким образом, существует бесчисленное множество точек пересечения.

Пример. Найти точку пересечения прямых и .

Решение. Решая совместно систему данных уравнений, получим координаты точки их пересечения

.

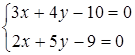Получаем Следовательно, прямые пересекаются в точке .

< Предыдущая		Следующая >