37. Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое Определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 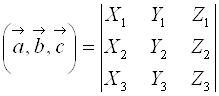 , или в свернутой форме
, или в свернутой форме 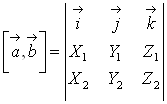 . Предыдущая формула получается разложением определителя по первой строке.
. Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу ![]() -го порядка
-го порядка
|
|
(9.2) |
Для записи определителя ![]() -го порядка матрицы
-го порядка матрицы ![]() будем применять обозначения
будем применять обозначения ![]() . При
. При ![]() матрица
матрица ![]() состоит из одного элемента и ее определитель равен этому элементу. При
состоит из одного элемента и ее определитель равен этому элементу. При ![]() получаем определитель
получаем определитель ![]() .
.
Минором ![]() элемента
элемента ![]() матрицы
матрицы ![]() называют определитель матрицы
называют определитель матрицы ![]() -го порядка, получаемого из матрицы
-го порядка, получаемого из матрицы ![]() вычеркиванием
вычеркиванием ![]() -той строки и
-той строки и ![]() -го столбца.
-го столбца.
Пример 7. Найти минор ![]() матрицы:
матрицы:
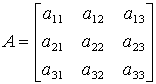 .
.
По определению, минор ![]() элемента
элемента ![]() есть определитель матрицы, получаемой из матрицы
есть определитель матрицы, получаемой из матрицы ![]() вычеркиванием первой строки и второго столбца. Следовательно,
вычеркиванием первой строки и второго столбца. Следовательно, 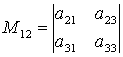 .
.
Алгебраическим дополнением элемента ![]() матрицы
матрицы ![]() называется минор
называется минор ![]() , взятый со знаком
, взятый со знаком ![]() . Алгебраическое дополнение элемента
. Алгебраическое дополнение элемента ![]() обозначается
обозначается ![]() , следовательно,
, следовательно, ![]() .
.
Пример 8. Найти алгебраическое дополнение элемента ![]() матрицы
матрицы ![]() из примера 7.
из примера 7.
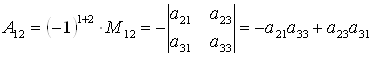 .
.
Определителем квадратной матрицы ![]()
![]() -го порядка
-го порядка ![]() называется число:
называется число:
|
|
(9.3) |
Где ![]() ‑ элементы первой строки матрицы (9.2), а
‑ элементы первой строки матрицы (9.2), а ![]() их алгебраические дополнения
их алгебраические дополнения![]() .
.
Запись по формуле (9.3) называется Разложением определителя по первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы ![]()
![]() -го порядка
-го порядка ![]() называется число:
называется число:
|
|
(9.4) |
Где ![]() ‑ элементы первого столбца матрицы (9.2), а
‑ элементы первого столбца матрицы (9.2), а ![]() их алгебраические дополнения
их алгебраические дополнения![]() .
.
Свойство 2. Если поменять местами две строки или два столбца матрицы ![]() , то ее определитель изменит знак на противоположный.
, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы ![]() -го порядка (будем в дальнейшем говорить определитель
-го порядка (будем в дальнейшем говорить определитель ![]() -го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
![]() , или
, или ![]() .
.
Свойство 3. Определитель, у которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе ![]() две одинаковые сроки местами. Тогда, по свойству 2 получим определитель
две одинаковые сроки местами. Тогда, по свойству 2 получим определитель ![]() , но с другой стороны, определитель не изменится, т. е.
, но с другой стороны, определитель не изменится, т. е. ![]() . Отсюда
. Отсюда ![]() .
.
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя ![]() умножить на число
умножить на число ![]() , то определитель умножится на
, то определитель умножится на ![]() .
.
![]() .
.
Умножим элементы ![]() -той строки на
-той строки на ![]() . Тогда получим определитель:
. Тогда получим определитель:
![]() .
.
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пропорциональны, равен нулю.
Пусть ![]() -я строка пропорциональна
-я строка пропорциональна ![]() -ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя ![]() есть сумма двух слагаемых, то определитель
есть сумма двух слагаемых, то определитель ![]() равен сумме двух определителей: у одного из них
равен сумме двух определителей: у одного из них ![]() -той строкой (столбцом)служат первые слагаемые, а у другого – вторые.
-той строкой (столбцом)служат первые слагаемые, а у другого – вторые.
Разложив определитель ![]() по
по ![]() -той строке получим:
-той строке получим:
![]()
![]() .
.
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам ![]() -той строки определителя
-той строки определителя ![]() соответствующие элементы
соответствующие элементы ![]() -ой строки, умноженные на число
-ой строки, умноженные на число ![]() , получим определитель
, получим определитель ![]() . Определитель
. Определитель ![]() равен сумме двух определителей: первый есть
равен сумме двух определителей: первый есть ![]() , а второй равен нулю, так как у него
, а второй равен нулю, так как у него ![]() -тая и
-тая и ![]() -тая строки пропорциональны.
-тая строки пропорциональны.
Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т. е.:

Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель ![]() , который получается из данного определителя
, который получается из данного определителя ![]() заменой
заменой ![]() -той строки
-той строки ![]() -той строкой. Определитель
-той строкой. Определитель ![]() равен нулю, так как у него две одинаковые строки. Разложив его по
равен нулю, так как у него две одинаковые строки. Разложив его по ![]() -той строке получим:
-той строке получим:
![]() .
.
Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т. е. ![]() .
.
| < Предыдущая | Следующая > |
|---|
