36. Операции над матрицами

Суммой двух матриц и одинакового размера называется матрица того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т. е. .

Сложение матриц обладает следующими свойствами:

1. Коммутативность, т. е. .

2. Ассоциативность, т. е. .

3. Для любых двух матриц и одинакового размера существует единственная матрица такая, что . Матрица обозначается и называется разностью матриц и . Уравнение имеет решение , получающаяся при этом матрица называется противоположной и обозначается .

Произведением матрицы на число называется матрица, все элементы которой равны соответствующим элементам матрицы , умноженным на число .

Умножение матрицы на действительное число обладает следующими свойствами:

1. ;

2. ;

3. ;

4. (ассоциативность);

5. (дистрибутивность);

6. (дистрибутивность).

Матрица называется Согласованной С матрицей , если число столбцов матрицы равно числу строк матрицы . В этом случае произведением матрицы на матрицу называется матрица , где , т. е. элемент, стоящий в -той строке и -том столбце матрицы произведения равен сумме произведений элементов -той строки матрицы на соответствующие элементы -го столбца матрицы .

Свойства умножения:

1. Если матрица согласована с матрицей , а матрица согласована с матрицей , то ‑ Ассоциативность умножения;

2. ‑ Свойство дистрибутивности;

3. Умножение матриц не коммутативно, т. е., как правило, .

Транспонированием матрицы называется операция замены местами строк и столбцов с сохранением порядка их следования, т. е. -я строка матрицы становится -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице обозначается .

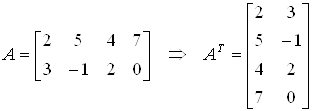
Свойства транспонирования:

< Предыдущая		Следующая >