11. Многочлены. Действия над многочленами

Выражение вида

(2.3)

Где

Называется Многочленом n-й степени от одной переменной Х, записанным в стандартном виде.

Числа Называются Коэффициентами дан­ного многочлена, – Старшим коэффициентом, – Свободным членом.

Если необходимо указать степень многочлена то пишут

Если то называется Приведенным многочленом.

Если кроме рассмотреть случай то многочлен вида называется Многочленом нулевой степени, он есть число.

Каждое слагаемое вида многочлена (2.3) называется Одночленом.

Два многочлена, заданные в виде (2.3), называются Равными, если равны все их коэффициенты при соответствующих степенях переменной Х.

Для всякого многочлена и многочлена определены следующие операции:

1) Умножение Многочленов на число

2) Сложение Многочленов:

3) Умножение Многочленов производят по следующему правилу: каждый член одного многочлена умножают на каждый член второго многочлена, полученные результаты складывают и приводят подобные;

4) деление Многочленов (при условии, что степень делителя меньше или равна степени делимого) выполняется по правилу «деления углом».

Результат деления записывается в виде:

или (2.4)

Где – частное (многочлен); – остаток (степень остатка меньше степени делителя).

Многочлен делится Нацело на если или

Если где то результат деления многочлена на согласно формуле (2.4), можно записать в виде равенства

(2.5)

Где R0 – число.

Коэффициенты многочлена

И остаток R0 в равенстве (2.5) можно вычислить по Схеме Горнера:

(2.6)

При вычислении коэффициентов (2.6) используют таблицу:

Х – х0	An	An-1	An-2	. . .	A1	A0
X0	Сn-1	СN-2	СN-3	. . .	С0	R0

Верхняя строка заполняется коэффициентами заданного многочлена (2.3), нижняя – числами, которые вычисляют по формулам (2.6).

Число называется Корнем многочлена если

Число называется Корнем кратности K многочлена если

и

Теорема 1 (Безу). Число х0 является корнем многочлена тогда и только тогда, когда делится нацело на

Теорема 2. Число является остатком от деления многочлена на тогда и только тогда, когда

Теорема 3. Пусть – приведенный многочлен с целыми коэффициентами. Если он имеет целые корни, то они содержатся среди целых делителей свободного члена.

Представление многочлена в виде произведения двух или нескольких многочленов (если это возможно) называется Разложением на множители.

Общий вид разложения на множители:

Где А, A1; …; АM; B1; …; Bm; C1; …; Cm  R (const);

Х1; Х2; …; Хk – корни многочлена

Квадратные трехчлены не имеют действительных корней.

Основные методы разложения:

1) вынесение общего множителя за скобки;

2) метод группировки:

- непосредственно;

- с предварительными преобразованиями слагаемых;

3) использование формул сокращенного умножения;

4) использование формул разложения квадратного трехчлена на множители

5) выделение полного квадрата и сведение к разности квадратов;

6) введение новой переменной;

7) поиск корней многочлена среди делителей свободного члена, использование теоремы Безу.

Многочлен может зависеть не только от одной переменной, но и от двух трех и т. д. Данные многочлены называются Многочленами от нескольких переменных. Тогда их Одночленом называют выражение, представляющее собой произведение чисел и переменных в некоторых степенях. Степенью Одночлена называют сумму показателей степеней всех входящих в него переменных. Старшая степень многочлена нескольких переменных определяется старшей степенью его одночлена.

Многочлен от двух переменных называется Симметрическим, если при замене переменных X На У и У на X Выражение не меняется.

Над многочленами от нескольких переменных можно выполнять действия, аналогичные действиям над многочленами от одной переменной. Для разложения данных многочленов на множители применяются те же методы, что и для Многочленов от одной переменной.

Пример 1. Представить многочлен в стандартном виде, определить его степень:

1) 2)

Решение. 1) Раскроем скобки и приведем подобные:

Данный многочлен является многочленом 2-й степени относительно Х.

2) Умножим многочлен на одночлен

Приведем подобные и получаем многочлен

Который является многочленом 5-й степени от двух переменных Х, У (наибольшее суммарное значение показателей имеем в первом одночлене: 2 + 3 = 5).

Пример 2. Найти частное и остаток от деления многочлена на многочлен Результат деления записать в виде равенства.

Решение. Воспользуемся правилом «деления углом»:

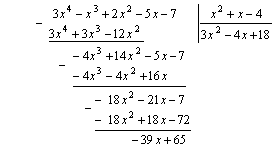
Получаем:

– частное (целая часть);

– остаток (многочлен 1-й степени).

Тогда

Пример 3. Проверить, делится ли многочлен нацело на Если нет, то найти значение остатка (не выполняя деления).

Решение. У данного многочлена свободный член есть число Поскольку число 5 не является делителем числа –3, то – не является корнем многочлена (см. теорему 3). Значит, согласно теореме 1, не разделится нацело на

Остаток находим по теореме 2.

Пример 4. Разложить многочлен на множители:

1) 2)

3) 4)

5) 6)

7)

Решение. 1) Используем метод вынесения общего множителя за скобки:

Поскольку у квадратного трехчлена то получен ответ.

2) Воспользуемся методом группировки:

Для дальнейшего разложения выделим полный квадрат и сведем к разности квадратов:

Поскольку дискриминанты квадратных трехчленов отрицательны, окончательно получаем разложение

3) Вначале преобразуем данное выражение, а затем используем метод группировки и формулу разности квадратов:

Вычисляем корни полученного квадратного трехчлена:

Поэтому

4) Вынесем общий множитель за скобки и воспользуемся формулой разности кубов:

Получили искомое разложение.

5) Для многочлена запишем целые делители свободного члена: (см. теорему 3). Подставим данные значения вместо убеждаемся, что является корнем, так как

Разделим заданный многочлен на

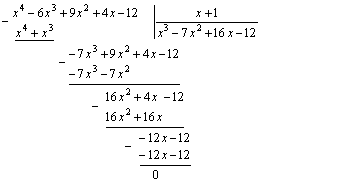
Получаем

Для многочлена выполним аналогичные действия.

Проверкой делителей свободного члена находим корень 2.

Делим:

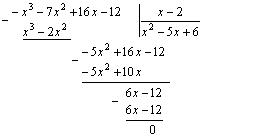
Тогда

Квадратный трехчлен разлагаем на множители, используя формулы корней. Окончательно получаем:

6) Для многочлена найдем целый корень среди делителей свободного члена Это число –1. Для дальнейшего разложения воспользуемся схемой Горнера:

Х3 Х2 Х1 Х0

Х + 1	1	6	11	6
-1	1	5	6	0

Х2 Х1 Х0

Таким образом, Квадратный трехчлен имеет корни и а потому окончательно получаем:

7) Для разложения многочлена воспользуемся методом введения новой переменной. Пусть Тогда имеем Корни этого многочлена – числа 4 и –2. Поэтому Возвращаясь к старой переменной, имеем

Пример 5. Найти A И B из заданного равенства и доказать, что A + B = 0:

Решение. Приведем правую часть заданного равенства к общему знаменателю:

или

Поскольку знаменатели дробей равны, приравняем числители и сгруппируем в правой части коэффициенты при Х. Многочлен в правой части запишем в стандартном виде:

Из определения равенства многочленов получаем систему и решаем ее:

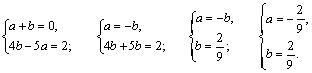
Находим сумму

Доказательство завершено.

< Предыдущая		Следующая >