07. Действия над комплексными числами в алгебраической форме

Пусть тогда:

(1.13)

(1.14)

(1.15)

Формулы (1.13)–(1.15) показывают, что операции сложения, вычитания и умножения выполняются аналогично таким же действиям над многочленами (с учетом при умножении).

Для нахождения частного комплексных чисел и сначала числитель и знаменатель дроби умножают на сопряженное знаменателю число а затем производят остальные действия:

(1.16)

Свойства комплексно-сопряженных чисел:

1) 2)

3) 4)

5) 6)

Пример 1. Найти и если

1) 2) 3)

Решение. 1) Так как то

2) Поскольку

3) Запишем число в стандартном виде: Поэтому

Пример 2. Даны комплексные числа и Найти:

1) 2) 3) 4)

Решение. 1)

2)

3) Перемножим числа и

4) Для нахождения частного умножим числитель и знаменатель дроби на (т. е. на число, сопряженное знаменателю). Тогда получим

Пример 3. Найти число, сопряженное числу

Решение. Умножив числитель и знаменатель дроби на получим

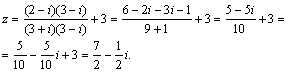
Тогда

Пример 4. Вычислить для N ΠN.

Решение. При вычислении используем, что, согласно определению, Тогда

Очевидно, что значения степени повторяются циклически:

Где .

Пример 5. Найти множество точек, для которых

Решение. Поскольку точки искомого множества лежат на прямой параллельной мнимой оси (рис. 1.11).

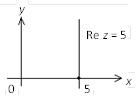
Рис. 1.11

Пример 6. Показать на координатной плоскости множество всех точек, которые находятся на расстоянии, равном 3, от точки

Решение. Пусть – одна из искомых точек. На плоскости ей соответствует точка с координатами Точке соответствует точка плоскости с координатами В качестве решения задачи подходят все точки, для которых

т. е.

Полученному уравнению соответствует множество точек окружности с центром в точке и радиусом 3 (рис. 1.12).

Рис. 1.12

< Предыдущая		Следующая >