05. Задания
I уровень
1.1. Пусть ![]()
![]()
![]() Найдите множество:
Найдите множество:
1) A È B; 2) A Ç B; 3) B È C; 4) B Ç C;
5) (A È B) Ç C; 6) A È (B Ç C); 7) A / (B Ç C).
1.2. Пусть А – множество натуральных делителей числа 15; В – множество простых чисел, меньших 10; С – множество четных чисел, меньших 9. Найдите множество:
1) A È B; 2) A Ç B; 3) B Ç C;
4) (A È C) Ç B; 5) A È (C Ç B); 6) A Ç B Ç C.
1.3. В группе учатся 28 студентов, каждый из которых умеет кататься на лыжах или коньках. При этом 20 человек умеют кататься на лыжах, 15 человек – на коньках. Определите, сколько студентов умеют кататься и на коньках, и на лыжах.
1.4. Задано некоторое количество натуральных чисел, которые кратны или числу 2, или числу 3. Известно, что числу 2 кратны 10 чисел; числу 3 кратны 7 чисел; и числу 2, и числу 3 кратны 4 числа. Определите общее количество заданных чисел.
1.5. Все 25 человек класса сходили в театр или кино. Известно, что 20 человек были в кино, 10 человек – и в театре, и в кино. Сколько человек было в театре?
1.6. Вычислите:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
1.7. Сократите дробь:
1) ![]() 2)
2) ![]()
1.8. Определите целую и дробную части числа:
1) 1,02; 2) –1,2; 3) ![]()
4) ![]() 5) –5,2; 6) 3,25.
5) –5,2; 6) 3,25.
1.9. Вычислите выражение:
1) ![]() 2)
2) ![]()
1.10. Запишите сумму, указав каждое слагаемое, и вычислите ее:
1) ![]() 2)
2) ![]() 3)
3) ![]()
II уровень
2.1. Запишите, с помощью каких операций над множествами A, B, C получено заштрихованное множество на рис. 1.9:
1) 2) 3)
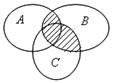
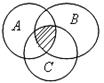
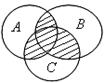
4) 5) 6)
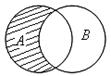
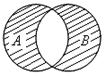
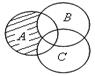
Рис. 1.9
2.2. Пусть ![]() – подмножества универсального множества U = R. Найдите множество:
– подмножества универсального множества U = R. Найдите множество:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2.3. Заданы множества:
![]()
![]()
![]()
Найдите множество:
1) A È B; 2) A Ç B; 3) B \ C;
4) A \ B; 5) A Ç B Ç C; 6) A È B È C.
2.4. В школе 1400 учеников. Из них 1250 умеют кататься на лыжах, 952 – на коньках. Ни на лыжах, ни на коньках не умеют кататься 60 учащихся. Сколько учащихся умеют кататься и на лыжах, и на коньках?
2.5. В группе из 100 туристов 70 человек знают английский, 45 французский и 23 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни французского языка?
2.6. В штучном отделе магазина посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и коробку конфет. В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?
2.7. В первом туре олимпиады участвовали 100 студентов, из них 70 человек получили право участвовать во втором туре олимпиады по физике, 45 – по математике. Известно, что 23 человека могут участвовать во втором туре и по физике, и по математике. Сколько студентов не допущено ко второму туру ни по физике, ни по математике?
2.8. Сравните дроби:
1) ![]() и
и ![]()
2) ![]() и
и ![]()
2.9. Сократите дробь и упростите полученное выражение:
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
III уровень
3.1. Для универсального множества R рассматриваются подмножества ![]()
![]() Найдите множество:
Найдите множество:
1) ![]() 2)
2) ![]() 3)
3) ![]()
3.2. Докажите включение:
1) ![]()
2) ![]()
3.3. Докажите равенство:
1) ![]()
2) ![]()
3.4. Среди абитуриентов, которые успешно выдержали вступительные экзамены в университет, оценку «отлично» получили: по математике – 48 человек; по физике – 37; по белорусскому языку – 42; по математике или физике – 75; по математике или белорусскому языку – 76; по физике или белорусскому языку – 66; по всем трем дисциплинам – 4. Выясните: 1) сколько абитуриентов получили хотя бы одну пятерку; 2) сколько человек получили только одну пятерку.
3.5. В школьной олимпиаде по математике участвовали 100 человек, по физике – 50, по информатике – 48. Когда учеников опросили, в скольких олимпиадах они участвовали, ответ «в двух» дали вдвое меньше человек, чем «в одной», а «в трех» - втрое меньше, чем «в одной». Сколько всего учеников участвовало в этих олимпиадах?
3.6. В олимпиаде по математике принимало участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну – по геометрии и одну – по тригонометрии. Результаты проверки работ представлены в таблице:
|
.Решены задачи |
Количество решивших |
|
По алгебре |
20 |
|
По геометрии |
18 |
|
По тригонометрии |
18 |
|
По алгебре и геометрии |
7 |
|
По алгебре и тригонометрии |
8 |
|
По геометрии и тригонометрии |
9 |
Известно также, что три человека не справились ни с одной задачей. Сколько учащихся решили все три задачи? Сколько решили ровно две задачи?
3.7. Из 100 абитуриентов на первом экзамене получили отличные и хорошие оценки 80 %, на втором экзамене – 72 %, на третьем – 60 %. Какое может быть наименьшее число абитуриентов, получивших отличные и хорошие оценки на всех трех экзаменах?
3.8. Выясните, при каком натуральном N справедливо неравенство и докажите его методом математической индукции:
1) ![]() 2)
2) ![]() 3)
3) ![]()
| < Предыдущая | Следующая > |
|---|