85. Взаимное расположение прямой и плоскости в пространстве
Пусть в пространстве прямя A, в некоторой аффинной системе координат задана параметрическими уравнениями:
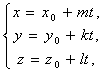 (1)
(1)
Плоскость a задана общим уравнением:
A: Ax + By + Cz + D = 0. (2)
Исследуем взаимное расположение прямой и плоскости. Для этого подставим из уравнений (1) в уравнения (2) и получим
A(X0 + Mt) + B(Y0 + Kt) + C(Z0 + Lt) + D = 0,
(Am + Bk + Cl)T + AX0 + By0 + Cz0 + D = 0. (3)
Отсюда и из теоремы о линейном уравнении получаем следующую теорему.
Теорема 1. Пусть дана прямая A и плоскость A, заданные соответственно уравнениями (1) И (2). Тогда справедливы следующие утверждения:
1) Прямая и плоскость пересекаются тогда и только тогда, когда
Am + Bk + Cl ≠ 0; (4)
2) Прямая и плоскость параллельны тогда и только тогда, когда
Am + Bk + Cl = 0, AX0 + By0 + Cz0 + D ≠ 0; (5)
5) Прямая и плоскость параллельны тогда и только тогда, когда
Am + Bk + Cl = 0, AX0 + By0 + Cz0 + D = 0. (6)
Пусть в пространстве прямя A, в некоторой прямоугольной системе координат задана каноническими уравнениями:
А: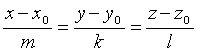
|
|
А плоскость a задана общим уравнением:
A: Ax + By + Cz + D = 0. (8)
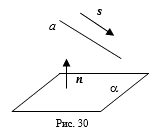
Определение 1. Углом, между прямой А И плоскостью a, Которые пересекаются, называется угол между прямой а и ее проекцией на плоскость A. Если прямая а и плоскость A параллельны, то угол считается равным нулю.
Рассмотрим угол b между направляющим вектором S = (M,K,L) - прямой А и нормальным вектором N = (A,B,C) плоскости a. Тогда угол j между прямой А и плоскостью a равен j=p ¤ 2 - b. Тогда из формулы для скалярного произведения векторов находим, что
Sin j = cos b =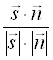 .
.
Отсюда находим, что
![]() . (9)
. (9)
Прямая А и плоскость a перпендикулярны тогда и только тогда, когда направляющий вектор S = (M,K,L) прямой A коллиниарен нормальному вектору N = (A,B,C) плоскости a. Последнее равносильно условию. Получаем Условие перпендикулярности прямой и плоскости
Am + Bk + Cl = 0. (10)
| < Предыдущая | Следующая > |
|---|