84. Расстояние между двумя прямыми
Определение 1. Расстоянием между двумя прямыми A И B Называется кратчайшее расстояние между точками этих прямых
Если прямые A и B пересекаются или совпадают, то расстояние между прямыми равно нулю. Если прямые параллельны или скрещиваются, то кратчайшее расстояние между ними равно длине общего перпендикуляра, проведенного к эти прямым.
Пусть прямые A и B в пространстве, в некоторой прямоугольной системе заданы каноническими уравнениями (1) и (2) из § 6. Эти прямые A и B задаются своими направляющими векторами S1 = (M1,K1,L1), S2 = (M2,K2,L2) и точками M1(X1,Y1,Z1), M2(X1,Y1,Z1) которые принадлежат этим прямым, вектор ![]() . Рассмотрим два случая.
. Рассмотрим два случая.
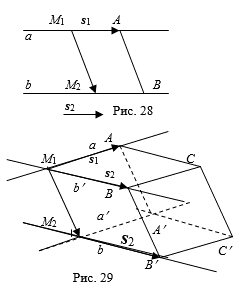
Прямые A и B Параллельны. Рассмотрим вектор ![]() = S1 и построим параллелограмм M1ABM2. Тогда расстояние D между прямыми A и B равно высоте H параллелограмма M1ABM2, опущенной на сторону M1A. По формуле площади S параллелограмма находим S = M1A× H. Далее по определению векторного произведения имеем S = |
= S1 и построим параллелограмм M1ABM2. Тогда расстояние D между прямыми A и B равно высоте H параллелограмма M1ABM2, опущенной на сторону M1A. По формуле площади S параллелограмма находим S = M1A× H. Далее по определению векторного произведения имеем S = |![]() |. Следовательно,
|. Следовательно,
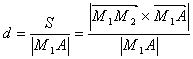 .
.
Подставляя сюда координаты векторов получаем, что расстояние между параллельными прямыми находится по формуле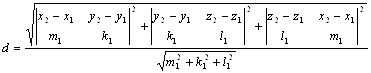 .
.
Прямые A и B Скрещиваются. Через точки M1 И M2 проведем прямые A¢ и B¢ параллельные соответственно прямым A и B. От точки M1 отложим векторы![]() ,
, ![]() = S1 и
= S1 и ![]() = S2, на этих векторах построим параллелепипед M1AСBM2A¢B¢С¢. Расстояние между прямыми A и B равно расстоянию между плоскостями, в которых лежат основания M1AСB, M2A¢B¢С¢ параллелепипеда, т. е. равно высоте H параллелепипеда. С одной стороны, объем параллелепипеда M1AСBM2A¢B¢С¢ можно вычислить по формуле: V = Sh, Где S - площадь основания M1AСB. С другой стороны, по свойству смешенного произведения V =
= S2, на этих векторах построим параллелепипед M1AСBM2A¢B¢С¢. Расстояние между прямыми A и B равно расстоянию между плоскостями, в которых лежат основания M1AСB, M2A¢B¢С¢ параллелепипеда, т. е. равно высоте H параллелепипеда. С одной стороны, объем параллелепипеда M1AСBM2A¢B¢С¢ можно вычислить по формуле: V = Sh, Где S - площадь основания M1AСB. С другой стороны, по свойству смешенного произведения V =![]() . По определению векторного произведения S =
. По определению векторного произведения S = ![]() . Отсюда получаем, что
. Отсюда получаем, что
 .
.
Подставляя сюда координаты векторов получаем, что расстояние между скрещивающимися прямыми находится по формуле:
 .
.
| < Предыдущая | Следующая > |
|---|