83. Угол между прямыми в пространстве
Определение 1. Углом между двумя прямыми Называется угол между пересекающимися прямыми, параллельными данным прямым.
Пусть две прямые A и B в пространстве, в некоторой прямоугольной системе заданы каноническими уравнениями (1) и (2) из § 6.
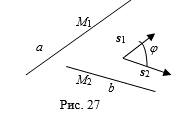
Угол J Между прямыми A и B равен углу между их направляющими векторами S1 = (M1,K1,L1), S2 = (M2,K2,L2). По определению скалярного произведения векторов
S1S2 = |S1|×| S2|cos J.
Отсюда находим формулу косинуса угла между прямыми A и B:
![]() . (3)
. (3)
Заметим, что прямыми A и B перпендикулярны тогда и только тогда, когда их направляющие векторы S1 и S2 ортогональны. По условию ортогональности векторов последнее равносильно тому, что скалярное произведение S1S2 = 0. Так как S1S2 = M1M2+K1K2+L1L2, то получаем теорему.
Теорема 2. Прямые A и B Перпендикулярны тогда и только тогда, когда
N1N2 = M1M2+K1K2+L1L2 = 0. (4)
| < Предыдущая | Следующая > |
|---|