82. Взаимное расположение прямых и плоскостей. Углы между прямыми
Пусть две прямые A и B в пространстве, в некоторой аффинной системе координат заданные каноническими уравнениями
A:![]() , (1)
, (1)
B:![]() . (2)
. (2)
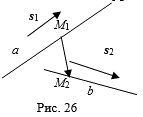
Эти прямые A и B задаются своими направляющими векторами S1 = (M1,K1,L1), S2 = (M2,K2,L2) и точками M1(X1,Y1,Z1), M2(X1,Y1,Z1) которые принадлежат этим прямым. Рас-сотрим вектор ![]() .
.
Рассмотрим матрицу, составленную из координат этих векторов,
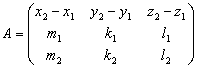 .
.
1. Прямые A и B скрещиваются тогда и только тогда, когда векторы ![]() , S1, S2 некомпланарны. Последнее равносильно тому, что det A Не равен нулю, т. е. rang A = 3.
, S1, S2 некомпланарны. Последнее равносильно тому, что det A Не равен нулю, т. е. rang A = 3.
2. Прямые A и B пересекаются тогда и только тогда, когда векторы ![]() , S1, S2 компланарны, а векторы S1 и S2 неколлинеарны. Последнее равносильно тому, что det A =0, а и вторая и третья строки матрицы A непропорциональны, т. е. rang A = 2, а ранг матрицы, составленной из двух последних строк равен 2.
, S1, S2 компланарны, а векторы S1 и S2 неколлинеарны. Последнее равносильно тому, что det A =0, а и вторая и третья строки матрицы A непропорциональны, т. е. rang A = 2, а ранг матрицы, составленной из двух последних строк равен 2.
3. Прямые A и B параллельны тогда и только тогда, когда векторы S1 и S2 коллинеарны, а векторы ![]() И S1 неколлинеарны. Последнее равносильно тому, что в матрице А вторая и третья строки пропорциональны, т. е. rang A = 2, а ранг матрицы, составленной из двух последних строк равен 1.
И S1 неколлинеарны. Последнее равносильно тому, что в матрице А вторая и третья строки пропорциональны, т. е. rang A = 2, а ранг матрицы, составленной из двух последних строк равен 1.
4. Прямые A и B совпадают тогда и только тогда, когда векторы ![]() , S1 и S2 попарно коллинеарны. Последнее равносильно тому, что все строки матрицы А попарно пропорциональны, т. е. rang A = 1.
, S1 и S2 попарно коллинеарны. Последнее равносильно тому, что все строки матрицы А попарно пропорциональны, т. е. rang A = 1.
Таким образом, доказана следующая теорема.
Теорема 1. Пусть прямые A и B заданы каноническими уравнениями (1) И (2). Тогда справедливы следующие утверждения:
1) A и B скрещиваются тогда и только тогда когда rang A = 3;
2) A и B пересекаются тогда и только тогда, когда rang A = 2, А вторая и третья строки матрицы A непропорциональны;
3) A И B Параллельны тогда и только тогда, когда rang A = 2, А вторая и третья строки матрицы A Пропорциональны;
7) A И B Совпадают тогда и только тогда, когда rang A = 1.
| < Предыдущая | Следующая > |
|---|