81. Различные уравнения прямой в пространстве
Пусть в пространстве задана аффинная система координат (O,E1,E2,E3) .
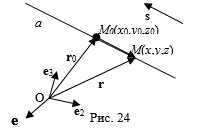
Определение 1. Направляющим вектором прямой A называется ненулевой вектор S, параллельный прямой A.
Пусть S = (M,K,L) -направляющие вектора прямой А, M0(X0,Y0,Z0)- точка, принадлежащая прямой А. Пусть M(X,Y,Z), произвольная точка пространства,
![]()
![]() .
.
Точка M принадлежит прямой А Тогда и только тогда, когда векторы ![]() И S коллинеарны. Последнее равносильно тому, что координаты этих векторов пропорциональны. Отсюда получаем Уравнение прямой, проходящей через точку M0(X0,Y0,Z0), параллельной вектору S = (M,K,L):
И S коллинеарны. Последнее равносильно тому, что координаты этих векторов пропорциональны. Отсюда получаем Уравнение прямой, проходящей через точку M0(X0,Y0,Z0), параллельной вектору S = (M,K,L):
![]()
|
|
Уравнение (1) называется Каноническим уравнением прямой. Заметим, что если знаменатель в каноническом уравнении равен нулю, то и соответствующий числитель равен нулю.
Пусть M1(X1,Y1,Z1) и M2(X2,Y2,Z2) - две различные точки, принадлежащие прямой А. В качестве направляющего вектора прямой А возьмем вектор ![]() . Тогда по формуле (1) получаем Уравнение прямой, проходящей через две точки:
. Тогда по формуле (1) получаем Уравнение прямой, проходящей через две точки:
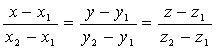 . (2)
. (2)
Рассмотрим радиус вектора RO = ![]() и R =
и R =![]() . Точка M принадлежит прямой А тогда и только тогда, когда векторы
. Точка M принадлежит прямой А тогда и только тогда, когда векторы ![]() = R - RO и S коллинеарны. Так как вектор S ненулевой, то последнее равносильно тому, что вектор R - RO линейно выражается через вектор S, т. е.
= R - RO и S коллинеарны. Так как вектор S ненулевой, то последнее равносильно тому, что вектор R - RO линейно выражается через вектор S, т. е.
R - RO = TS,
Где T - действительное число.
Отсюда получаем так называемое Векторно-параметрическое уравнение плоскости:
R = RO + TS, (3)
Где T - произвольный действительный параметр.
Так как R =![]() = (X,Y,Z), RO =
= (X,Y,Z), RO = ![]() = (X0,Y0,Z0), то запишем это уравнение в координатной форме. Получим Параметрические уравнения прямой прямой А:
= (X0,Y0,Z0), то запишем это уравнение в координатной форме. Получим Параметрические уравнения прямой прямой А:
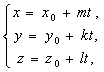 (4)
(4)
Где T - произвольный действительный параметр, S = (M,K,L) - направляющий вектор прямой А, M0(X0,Y0,Z0) - точка, принадлежащая прямой А.
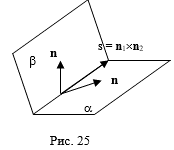
Прямую можно также представить как линию пересечения двух пересекающихся плоскостей a и b:
![]() , (5)
, (5)
Где A12 + B12+ C12 ≠ 0, A22 + B22+ C22 ≠ 0;
![]()
Чтобы перейти от уравнений (4) прямой к каноническим уравнениям прямой необходимо найти точку M0 этой прямой и направляющий вектор этой прямой. Решив систему (4) и найдем одно ее частное решение (X0,Y0,Z0), M0(X0,Y0,Z0)- точка, принадлежащая прямой А.
Наиболее легко направляющий вектор прямой находится в прямоугольной системе координат исходя из определения векторного произведения векторов. Для этого рассмотрим нормальные вектора N1 = (A1,B1,C1), N2 = (A2,B2,C2) плоскостей a и b. Направляющим вектором прямой пересечения плоскостей a и b является векторное произведение векторов N1 , N2.
Находим векторное произведение векторов
N1 ´ N2 = 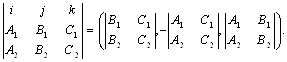 .
.
Таким образом, каноническое уравнение прямой (4) имеет вид:
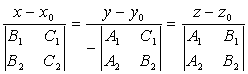 . (5)
. (5)
| < Предыдущая | Следующая > |
|---|