80. Геометрический смысл неравенства Ax + By + Cz + D ³ 0

В пространстве рассматривается произвольная аффинная система координат.

Теорема 2. Множество всех точек пространства, координаты которых удовлетворяют неравенству

Ax + By + Cz + D ³ 0 (2)

A2 + B2+ C2 ≠ 0, Является полупространством, ограниченным плоскостью

A: Ax + By + Cz + D = 0 (3)

В которой лежит конец вектора N = (A,B,C), Отложенного от произвольной точки плоскости a.

Доказательство. 1. Сначала покажем, что функция F(X,Y,Z) = Ax + By + Cz + D принимает значения одинаковых знаков, в точках каждой из полупространств, на которые плоскость a разбивает пространство.

Пусть M1(X1,Y1,Z1), M2(X2,Y2,Z2) любые две точки пространства, не принадлежащие плоскости a, и которые не лежат на прямой параллельной плоскости a. Тогда прямая M1M2 пересекает плоскость a в точке M(X,Y,Z), которая делит отрезок в некотором отношении l. Координаты точки M вычисляются по формулам:

(4)

И удовлетворяют уравнению плоскости a. Тогда справедливо равенство

Отсюда находим

.

Так как точка M2 Ïa, то . Тогда

.

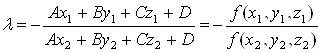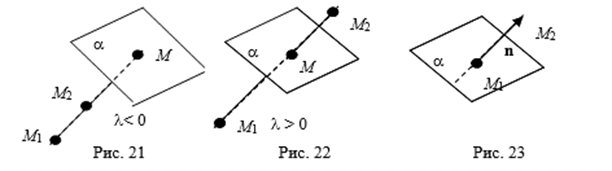
Точки M1 и M2 лежат по одну сторону от плоскости a тогда и только тогда, когда точка M не принадлежит отрезку M1M2. Последнее верно тогда и только тогда, когда l < 0. Следовательно, точки M1 и M2 лежат по одну сторону от плоскости a тогда и только тогда, когда функция F(X,Y,Z) принимает в точках M1 и M2 значения одного знака (см. рис 21).

Точки M1 и M2 лежат по разные стороны от плоскости a тогда и только тогда, когда точка M принадлежит отрезку M1M2. Последнее верно тогда и только тогда, когда l > 0. Следовательно, точки M1 и M2 лежат по разные стороны от плоскости a тогда и только тогда, когда функция F(X,Y,Z) принимает в точках M1 и M2 значения разных знаков (см. рис 22).

Если точки M1(X1,Y1,Z1), M2(X2,Y2,Z2) лежат на прямой параллельной плоскости a, то они также расположены по одну строну от плоскости a. Для того, чтобы это доказать, необходимо взять еще одну точку M2(X3,Y3,Z3) в том же полупространстве, не лежащую на прямой M1M2. В силу доказанного функция F(X,Y,Z) принимает в точках M1 и M3, M2 и M2 значения одного знака. Тогда в точках M1 и M2 функция принимает значения одного знака.

Таким образом, функция F(X,Y,Z) принимает значения одного знака в каждом из полупространств, на которые плоскость a разбивает пространство, и в разных полупространствах эти знаки различны.

2. Отложим, от точки M1(X1,Y1,Z1)€a вектор N = (A,B,C) и получим такую точку M2(X2,Y2,Z2), что = N = (A,B,C) (см. рис 23). Отсюда X2 = X1 + A, Y2 = Y1 + B, Z2 = Z1 + C. Подставим координаты точки M2 в левую часть уравнения (2) и получим

F(X2,Y2,Z2) = Ax2 + By2 + Cz2 + D = A(X1 + A) + B(Y1 + B) + C(Z1 + C)+ D =

= Ax1 + By1 + Cz1+ D + A2 + B2 + C2.

. Так как точка M1(X1,Y1,Z1)€a. то Ax1 + By1 + Cz1+ D = 0. Поэтому

F(X2,Y2,Z2) = A2 + B2 + C2 > 0.

< Предыдущая		Следующая >