79. Расстояние от точки до плоскости. Геометрический смысл неравенства Ax + By + Cz + D ³ 0

Определение 1. Расстоянием от точки M0 До плоскости A Называется длина перпендикуляра, опущенного из точки M0 На плоскость a.

Вычислим расстояние от точки M0(X0,Y0,Z0) до плоскости a, заданной в прямоугольной системе координат общим уравнением

A: Ax + By + Cz + D = 0, A2 + B2+ C2 ≠ 0.

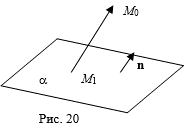
Отпустим из точки M0(X0,Y0,Z0) перпендикуляр M0M1 на плоскость a, M1 - основание перпендикуляра. Рассмотрим вектор

И нормальный вектор N = (A,B,C) плоскости. Так как векторы И N ортогональны одной и той же плоскости, то он коллинеарны. Вычислим их скалярное произведение двумя способами.

С одной стороны, так как угол j между векторами и N равен 0 или 1800, по определению скалярного произведения имеем × N = |N|× Cos j = ± |N| = ±D|N|, где D расстояние от точки M0 до плоскости a.

С дугой стороны,

× N = A(X0 - X1) + B(Y0 - Y1) +C(Z0 - Z1) =

= Ax0 + By0 +Cz0 + (-Ax1 - B y1 -C z1)

Так как точка M1€ a, то-Ax1 - B Y1 -C Z1 = D. Отсюда

±D|N| == Ax0 + By0 +Cz0 + D.

Таким образом, находим формулу расстояния от точки до плоскости

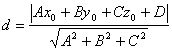. (1)

< Предыдущая		Следующая >