78. Угол между плоскостями

Определение 1. Углом между пересекающимися плоскостями называется величина любого из двухгранных углов, который образуется при пересечении плоскостей.

Пусть a и b две плоскости, заданные своими общими уравнениями в прямоугольной системе координат:

A: A1X + B1Y + C1Z + D1 = 0,

B: A2X + B2Y + C2Z + D2 = 0,

A12 + B12+ C12 ≠ 0, A22 + B22+ C22 ≠ 0.

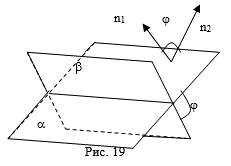
Рассмотрим нормальные векторы N1 = (A1,B1,C1), N2 = (A2,B2,C2) плоскостей a и b. В силу теоремы об углах с соответственно перпендикулярными сторонами угол j между плоскостями a и b равен углу между нормальными векторами N1 и N2. По определению скалярного произведения векторов

N1N2 = |N1|×| N2|cos J.

Отсюда находим формулу косинуса угла между плоскостями a и b:

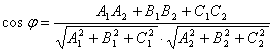. (6)

Заметим, что плоскости a и b перпендикулярны тогда и только тогда, когда нормальные векторы N1 и N2 этих плоскостей ортогональны. По условию ортогональности векторов последнее равносильно тому, что скалярное произведение N1N2 = 0. Так как N1N2 = A1A2+B1B2+C1C2, то получаем теорему.

Теорема 2. Плоскости a И b Перпендикулярны тогда и только тогда, когда

N1N2 = A1A2+B1B2+C1C2 = 0. (7)

< Предыдущая		Следующая >