75. Различные уравнения плоскости

Пусть в пространстве R 3 Задана прямоугольная система координат Oxyz.

Определение 1. Нормальным вектором плоскости A называется любой ненулевой вектор N Перпендикулярный плоскости A.

Пусть N = (A,B,C) ≠ 0, - нормальный вектор плоскости a, M0(X0,Y0,Z0)- точка, принадлежащая плоскости a. Пусть M(X,Y,Z), произвольная точка пространства,

.

Тогда точка M принадлежит плоскости a тогда и только тогда, когда векторы и N Ортогональны. Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, Последнее в ортонормированном базисе можно записать в виде:

A(X - X0) + B(Y - Y0) +C(Z - Z0) = 0 . (1)

Таким образом, получаем уравнение плоскости, Проходящей через точку и перпендикулярной вектору N = (A,B,C) ≠ 0.

Рассмотрим произвольное уравнение первого порядка

Ax + By + Cz + D = 0, (2)

Где коэффициенты одновременно не равны нулю, т. е. A2+ B2+ C2 ≠ 0.

Теорема 1. Любую плоскость в произвольной аффинной системе координат можно задать уравнением (1) первого порядка и обратно любое уравнение (1) первого порядка в аффинной системе координат определяет плоскость.

Доказательство. Достаточно доказать теорему для прямоугольной системы координат. Любую плоскость в прямоугольной системе координат можно задать ее нормальным вектором N = (A,B,C) ≠ 0 И точкой M0(X0,Y0,Z0), принадлежащей плоскости. Уравнение этой плоскости выведено в §2.2 и имеет вид:

A(X - X0) + B(Y - Y0) +C(Z - Z0) = 0.

Отсюда получаем

Ax + By +Cz +(-Ax0 - By0 - Cz0)= 0,

Ax + By +Cz + D= 0,

Где D = -Ax0 - By0 - Cz0. Так (A,B,C) ≠ 0, то A2+ B2+ C2 ≠ 0 и любая плоскость есть поверхность первого порядка.

Обратно, пусть некоторая поверхность в пространстве определена уравнением (1). Так как не все коэффициенты равны нулю, то уравнение (1) имеет решение (X0,Y0,Z0). Тогда

Ax0 + By0 + Cz0 + D = 0, (3)

И точка M0(X0,Y0,Z0) принадлежит поверхности. Вычитая почленно из уравнения (1) равенство (2), получим уравнение

A(X - X0) + B(Y - Y0) +C(Z - Z0) = 0,

Равносильное уравнению (1). Это уравнение в силу §2.2, определяет плоскость, проходящую через точку M0(X0,Y0,Z0), перпендикулярную вектору N = (A,B,C).

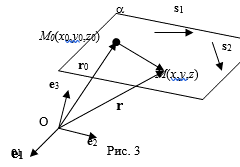
Определение 2. Направляющими векторами плоскости A называется пара неколлинеарных векторов S1 И S2 Параллельных плоскости A.

Пусть S1 = (M1,K1,L1), S2 = (M2,K2,L2) - направляющие вектора плоскости a, M0(X0,Y0,Z0)- точка, принадлежащая плоскости a. Пусть M(X,Y,Z), произвольная точка пространства,

.

Тогда точка M принадлежит плоскости a тогда и только тогда, когда векторы , S1 и S2 компланарны. Три вектора компланарны тогда и только тогда, когда определитель, составленный из координат этих векторов равен нулю. Таким образом, получаем уравнение плоскости по Двум направляющим векторам и точке, принадлежащей плоскости

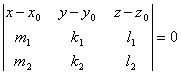. (4)

Пример 1. Найдем уравнение плоскости с направляющими векторами S1 = (B,-A,0), S2 = (C,0,-A), где A ≠ 0. Так как векторы S1 и S2 неколлинеарны, то формуле (4) находим уравнение этой плоскости:

.

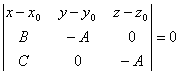Отсюда находим

.

Сократим на A ≠ 0 и получаем уравнение

. (5)

Рассмотрим радиус вектора RO = и R =. Точка M принадлежит плоскости a тогда и только тогда, когда векторы = R - RO, S1 и S2 компланарны. Так как векторы S1 и S2 неколлинеарны, то последнее равносильно тому, что вектор R - RO линейная комбинация векторов S1 и S2, т. е. R - RO = US1 +VS2, где U, V - действительные числа.

Отсюда получаем так называемое Векторно-параметрическое уравнение Плоскости.

R = RO + US1 +VS2, (6)

Где U, V - произвольные действительные параметры.

Так как R == (X,Y,Z), RO = = (X0,Y0,Z0), то запишем это уравнение в координатной форме. Получим Параметрические уравнения плоскости:

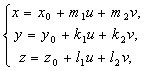(7)

Где U, V - произвольные действительные параметры, S1 = (M1,K1,L1), S1 = (M2,K2,L2) - направляющие вектора плоскости, M0(X0,Y0,Z0)- точка, принадлежащая плоскости.

Пусть даны три точки M1(X1,Y1,Z1), M2(X2,Y2,Z2), M3(X3,Y3,Z3) плоскости, которые не принадлежат одной прямой. Тогда векторы ,

являются направляющими векторами плоскости a. Применяя формулу (4) получим Уравнение плоскости, проходящей через три данные точки:

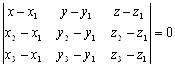. (8)

Пусть плоскость не проходит через начало координат и пересекает оси Ox, Oy, Oz Соответственно в точках M1(A,0,0), M2(0,B,0), M3(0,0,c). По формулу (8) находим уравнение плоскости, проходящей через эти три точки

.

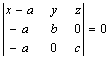Вычислим этот определитель и преобразуем полученное уравнение к более простому виду

(X - a)Bc + Yac + Zab = 0,

Xbc + Yac + Zab = Abc,

. (9)

Уравнение (5) называется Уравнением плоскости в отрезках на осях.

.Замечание 1. Уравнение (1) называется Общим уравнением плоскости. Если плоскость a задается общим уравнением (1) в прямоугольной системе координат, то N = (A,B,C) - нормальный вектор плоскости a.

Если плоскость a задается общим уравнением (1) в произвольной аффинной системе координат и A ≠ 0, то S1 = (B,-A,0), S2 = (C,0,-A) направляющие вектора плоскости a.

Рассмотрим Частные случаи уравнения (1).

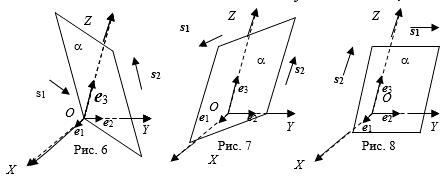
1. Пусть D = 0. Тогда уравнение (1) принимает вид: Ax + By + Cz = 0 и плоскость, определяемая этим уравнением, проходит через начало координат (см. Рис. 6).

2. Пусть С = 0, A ≠ 0. Тогда уравнение (1) принимает вид: Ax + By + D = 0. Рассмотрим направляющие вектора S1 = (B,-A,0) и S2 = (0,0,-A) этой плоскости. Так как базисный вектор Е3 = (0,0,1) оси Oz. коллинеарен вектору S2, то плоскость a, определяемая этим уравнением, параллельна оси Oz (см. Рис. 7).

3. Пусть B=0, С = 0, A ≠ 0. Тогда уравнение (1) принимает вид: Ax + D = 0. Рассмотрим направляющие вектора S1 = (0,-A,0) и S2 = (0,0,-A) этой плоскости. Так как базисные векторы е2 = (0,1,0), Е3 = (0,0,1) .коллинеарны соответственно векторам вектору S1, S2, то плоскость a, определяемая этим уравнением, параллельна координатной плоскости Ozy (см. Рис. 8).

< Предыдущая		Следующая >