76. Взаимное расположение плоскостей. Углы между плоскостями
Теорема 1. Пусть a И b Две плоскости, заданные своими общими уравнениями в аффинной системе координат:
A: A1X + B1Y + C1Z + D1 = 0,
B: A2X + B2Y + C2Z + D2 = 0,
A12 + B12+ C12 ≠ 0, A22 + B22+ C22 ≠ 0;
![]() .
.
Тогда справедливы утверждения:
4) Плоскости A и b Пересекаются тогда и только тогда, когда
Rang A = rang A¢ = 2;
5) Плоскости A и b Параллельны тогда и только тогда, когда
Rang A = 1, rang A¢ = 2;
6) Плоскости A и b Совпадают тогда и только тогда, когда
Rang A = Rang A¢ = 1.
Доказательство. Рассмотрим систему линейных уравнений:
![]() (1)
(1)
Применим к исследованию системы (1) теорему Кронекера-Капелли.
Рассмотрим матрицу и расширенную матрицы системы (1):
![]() .
.
Так как матрица А ненулевая, то rang A ³ 1. Имеем rang A¢ = rang A¢¢, rang A £ rang A¢ £ 2. Тогда возможны следующие случаи:
1) rang A = rang A¢ = 2. По теореме Кронекера - Капелли система (1) разрешима и плоскости a и b имеют общие точки. Так как при решении системы (1) методом Гаусса число свободных неизвестных равно 1, а не двум, то не все решения системы (1) являются решениями первого уравнения системы и плоскости a и b не совпадают. Следовательно, плоскости a и b Пересекаются.
2) rang A = 1, rang A¢ = 2. Тогда система (1) не имеет решений, и плоскости a и b не имеют общих точек, а поэтому Параллельны.
6) rang A = rang A¢ = 1. Тогда при приведении системы (1) к ступенчатому виду в системе останется одно из уравнений исходной системы, и система равносильна одному из уравнений системы (1). Следовательно, множество решений системы (1) совпадает с множеством решений одного из уравнений системы (1) и плоскости a и b Совпадают.
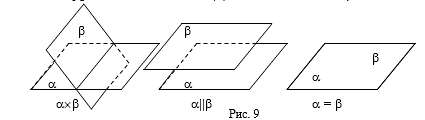
Обратные утверждения легко доказываются методом от противного. Пусть плоскости пересекаются. Докажем, что rang A = rang A¢ = 2. Допустим противное. Тогда rang A = 1, rang A¢ = 2 или rang A = rang A¢ = 1. Отсюда, по доказанному выше, a || b или a = b. Получаем противоречие с условием. Следовательно, допущение неверно и rang A = rang A¢ = 2. Аналогично рассматриваются случаи a || b или a = b.
Нетрудно проверить, что ранг двухстрочной матрицы равен 1 тогда и только тогда, когда ее строки пропорциональны (проверьте самостоятельно). Тогда из теоремы 1 получаем следующее следствие.
Следствие. 1) Плоскости A и b Пересекаются тогда и только тогда, когда коэффициенты при соответствующих неизвестных в уравнениях плоскостей непропорциональны:
![]() (2)
(2)
2) Плоскости A и b Параллельны тогда и только тогда, когда коэффициенты при соответствующих неизвестных в уравнениях плоскостей пропорциональны и не пропорциональны свободным членам:
![]() . (3)
. (3)
3) Плоскости A И b Совпадают тогда и только тогда, когда коэффициенты при соответствующих неизвестных в уравнениях плоскостей пропорциональны и пропорциональны свободным членам:
![]() . (4)
. (4)
Замечание 1. Совпадающие плоскости в некоторых случаях считаются также и параллельными, и в этом случае Условие параллельности плоскостей может быть записано в виде:
![]() .
.
| < Предыдущая | Следующая > |
|---|