74. Плоскость и прямая в пространстве. Уравнения поверхности в пространстве. Уравнение сферы

Определение 1. Пусть F(X,Y,Z) - Функция от трех действительных переменных X, Y, Z И в пространстве задана аффинная система координат . Уравнение

F(X,Y,Z) = 0 (1)

Называется Уравнением поверхности s В данной системе координат, если выполняются два условия:

3) Координаты X,Y,Z любой точки M(X,Y,Z) €s Удовлетворяют уравнению (11);

4) Если координаты X,Y,Z Точки M(X,Y,Z) Удовлетворяют уравнению (11), То точка M(X,Y,Z) €s.

Таким образом, M(X,Y,Z)€s тогда и только тогда, когда F(X,Y,Z)= 0.

Если F(X,Y,Z) многочлен степени N, то поверхность s называется Поверхность N - Го порядка.

Основными задачами аналитической геометрии в пространстве являются следующие задачи:

4) по определению поверхности составить ее уравнение в заданной пространственной системе координат;

5) по уравнению поверхности изучить ее свойства, установить вид поверхности и изобразить ее.

Определение 2. Сферой с центром в точке C Радиуса R Называется геометрическое место всех точек пространства, для каждой из которых расстояние до точки C равно R.

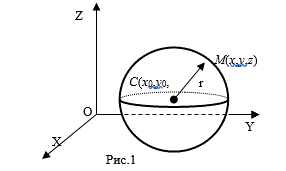
Обозначим сферу с центром в точке C радиуса символом S(C,R).

Выведем уравнение сферы в данной прямоугольной системе координат Oxyz. Пусть C(X0,Y0,Z0). По определению сферы точка M(X,Y,Z) принадлежит сфере с центром в точке C радиуса R тогда и только тогда, когда

|CM| = R. (2)

По формуле расстояния между двумя точками равенство (2) можно представить в виде:

.

Возведем в квадрат обе части полученного уравнения и находим уравнение сферы:

, (3)

Которое равносильное первоначальному.

Если центр сферы совпадает с началом координат, то уравнение (3) принимает вид:

. (4)

С помощью систем уравнений и неравенств могут быть в пространстве определены различные пространственные тела.

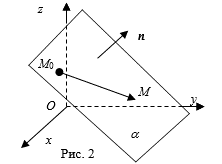
Определение 3. Шаром с центром в точке C Радиуса R Называется геометрическое место всех точек пространства, для каждой из которых расстояние до точки C не больше R.

Шар с центром в точке C(X0,Y0,Z0) радиуса R Задается неравенством

.

< Предыдущая		Следующая >