73. Конические сечения
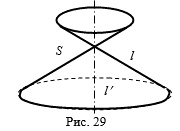
Определение 1. Пусть в пространстве даны две прямые A и B пересекающиеся в точке S. Круговой конической поверхностью называем поверхность, которая получается вращением, прямой A относительно прямой B. Прямая A называется Образующей, B- Осью, точка S - Вершиной конической поверхности (см. рис. 29).
Докажем теорему.
Теорема 1. Любое сечение конической поверхности плоскостью, не проходящей через вершину конической поверхности кривая второго порядка.
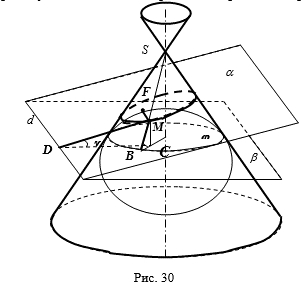
Доказательство. Пусть плоскость a не проходит через вершину S пересекает коническую поверхность по линии L (на рис.2 плоскость a пересекает все образующие одной половины конической поверхности). Предполагаем, что плоскость a не перпендикулярна оси конической поверхности. Действительно, если плоскость a перпендикулярна оси конической поверх
|
|
Возьмем произвольную точку M на линии L. Соединим точку с точками и. Прямая пересекает окружность в точке. По свойству касательных, проведенных из одной точки к окружности |MF| = |MB|. Пусть C - проекция точки на плоскость, D - проекция точки на прямую, g и j соответственно угол между плоскостями a и b и угол между плоскостью b и образующими конической поверхности.. Тогда имеем
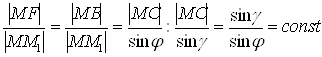. (1)
По теореме 1 § 8, что линия L является кривой второго порядка с фокусом.
Из формулы (1) следует, что эксцентриситет кривой второго порядка, лежащей в коническом сечении находится по формуле 
. Далее монотонно возрастающая функция в первой четверти. Отсюда получаем:
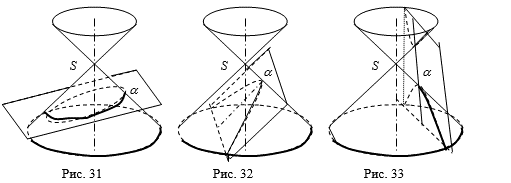
Если 0< e < 1, то g < j, и в сечении получается Эллипс. Это будет в случае, когда сечение a пересекает все образующие одной половины конической поверхности (см. рис 31).
Если e = 1, то g = j, и в сечении получается Парабола. Это будет в случае, когда сечение a параллельно одной из образующих конической поверхности (см. рис 32)..
Если 0< e < 1, то g > j, и в сечении получается Гипербола. Это будет в случае, когда сечение a пересекает обе половины конической поверхности (см. рис 33).
| < Предыдущая | Следующая > |
|---|
