71. Директориальные свойства эллипса, гиперболы и параболы
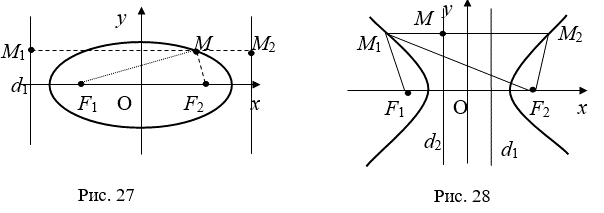
Определение 1. Директрисами эллипса и гиперболы Называются две прямые, параллельные оси OY канонической системы координат, и отстоящие от нее на расстоянии 
, - длина большой (действительно) полуоси, e - эксцентриситет соответствующей кривой. Директриса, расположенная по туже сторону от оси OY, что и фокус F называется соответственной фокусу F.
|
|
Канонические уравнения эллипса, гиперболы и параболы имеют степень 2, поэтому эти кривые являются Кривыми второго порядка. Под кривой второго порядка в этом и следующем параграфах мы понимаем именно только три указанные вида кривых. Тогда справедлива следующая теорема.
Теорема 1(Директориальное свойство). Кривая второго порядка (Эллипс гипербола, парабола) Есть множество всех точек плоскости, для каждой из которых отношение расстояния до фокуса F К расстоянию до соответствующей директрисы D Постоянно и равно эксцентриситету e.
Доказательство. Докажем утверждение теоремы для фокуса F1 и соответствующей директрисы d1 эллипса. Пусть M(X,Y) произвольная точка эллипса, M1 проекция точки M на директрису. Точка M1 имеет координаты: M1(- A/E, y). Вычислим расстояния. По формуле (4) § 1 |MF1| =
. Далее |MM1|=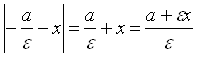
. Поэтому 
.
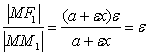Обратно M(X,Y) произвольная точка плоскости, M1 проекция точки M на директрису и 
. Имеем |MF1| =
, |MM1|= =
. Отсюда находим
=
.
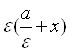Преобразуя это уравнение и возводя обе части его в квадрат, получаем
.
Так как 
, то полученное уравнение преобразуем к виду
Так как 
, то приходим к выводу, что координаты точки M удовлетворяют уравнению эллипса, и она принадлежит эллипсу.
Упражнение 1. Проверьте справедливость утверждения теоремы для фокуса F2 и директрисы d2. Докажите теорему для гиперболы и параболы.
Замечание 1. Утверждение теоремы по сути дает общее определение кривой второго порядка.
| < Предыдущая | Следующая > |
|---|
