69. Асимптоты гиперболы по каноническому уравнению. Равносторонняя гипербола. Эксцентриситет гипербол

Определение 1. Прямая называется Асимптотой линии L, Если точка по линии L, двигаясь к бесконечности, неограниченно приближается к данной прямой.

Теорема 1. Асимптотами гиперболы, заданной каноническим уравнением (3) из § 6, являются прямые .

Доказательство. В силу симметрии гиперболы относительно осей координат достаточно доказать теорему для прямой D: и точек гиперболы, лежащих в первой четверти, где она задается уравнением .

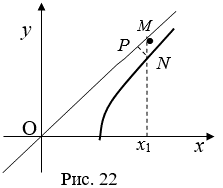
Рассмотрим произвольную прямую X=X1, которая пересекает эллипс в точке M(X1,y1), где , а прямую D в точке N(X1,y2), где .

Так как , то точка M лежит выше точки N. Пусть MP перпендикуляр, опущенный из точки M, на прямую D. Тогда имеем

.

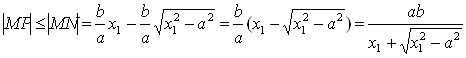Если X1 , то точка M стремится по гиперболе к бесконечности. При этом длина отрезка MP стремится к нулю, и прямая D является асимптотой.

Определение 2. Эксцентриситетом e гиперболы называется число, равное отношению его фокального расстоянию С к длине его действительной полуоси A: .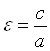

Из определения гиперболы следует, что e > 1. Для окружности эксцентриситет равен нулю.

Так как , то 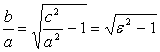. Из этого соотношения получаем, что чем ближе e к 1, тем меньше отношение B/A, и тем меньше угол между осью OX И асимптотами, чем больше e, тем больше отношение B/A, и тем больше между осью OX И асимптотами.

Определение 3. Гипербола называется Равносторонней, если у нее действительная и мнимая полуоси равны, т. е. A = B.

Покажем, что обычная школьная гипербола, которая является графиком функции , является равносторонней. Запишем его в виде Xy = K и повернем систему координат OXy на угол по формулам:

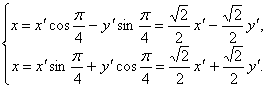
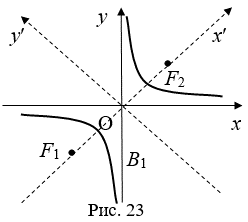
Получим ее уравнение в новой системе координат OX¢Y¢

Или

.

Таким образом, график обратной пропорциональности равнобочная гипербола.

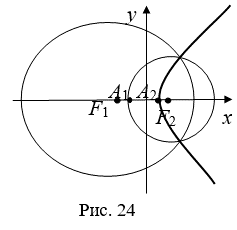
Замечание 1. С помощью циркуля и линейки можно построить сколь угодно много точек на гиперболе. Пусть действительная ось гиперболы A1A2, фокусы гиперболы F1, F2. Для этого произвольным радиусом R начертим окружность с центром в точке F2, и радиусом R + 2A с центром в точке F1. Точки пересечения окружностей лежат на гиперболе (см. рис. 24).

< Предыдущая		Следующая >