67. Гипербола. Каноническое уравнение гиперболы

Определение 1. Гиперболой Называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек F1 и F2 той же плоскости есть величина постоянная, меньшая, чем расстояние между точками F1, F2.

Точки называются Фокусами, расстояние |F1F2| называется Фокальным расстоянием. Обозначаем его через 2С. Через 2А обозначим модуль разности от любой точки гиперболы до фокусов. По определению A < C.

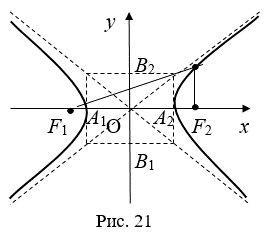
Выведем уравнение гиперболы в прямоугольной системе координат OXy, связанной с гиперболой. Для этого начало O системы координат поместим в середину отрезка F1F2, ось OX направим по прямой F1F2. Такая система координат называется Канонической. В выбранной системе координат фокусы имеют координаты F1(-C, 0) и F2(C, 0) .

Пусть M(X,Y) произвольная точка плоскости OXy. По определению 1 точка M принадлежит гиперболt тогда и только тогда, когда |MF1| - |MF2| = ±2C. (1)

Находим

|MF1| =, |MF2| =.

Отсюда получим уравнение гиперболы

. (2)

Для того, чтобы упростить это уравнение, запишем его в виде

И возведем обе его части в квадрат

Или

Возведя полученное уравнение в квадрат, находим:

Или

Обозначаем

И найденное выше уравнение запишем в виде

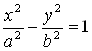. (3)

Мы доказали, что если точка лежит на гиперболе, то ее координаты удовлетворяют уравнению (3). Докажем обратное, что если координаты точки M(X,Y) удовлетворяют уравнению (3), то она принадлежит гиперболе. Для этого вычисляем расстояния |MF1| и |MF2|.

|MF1| ==

.

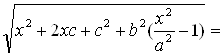
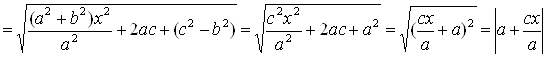Из уравнения (3) получаем 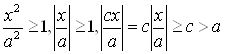, , 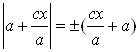где знак перед скобками совпадает со знаком X. Тогда

|MF1| = . (4)

Аналогично выводим, что

|MF2| =. (5)

Поэтому ||MF1| +|MF2|| = .

Таким образом, доказали, что уравнение (3) является уравнением гиперболы.

Уравнение (3) называется Каноническим уравнением гиперболы. Отрезки |MF1|, |MF2| называются Фокальными радиусами точки M.

< Предыдущая		Следующая >