66. Эллипса и окружность. Эксцентриситет эллипса

Теорема 1. Любой эллипс, отличный от окружности может быть получен в результате сжатия окружности к диаметру.

Доказательство. Рассмотрим окружность с центром в точке О радиуса А, заданную уравнением 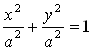. Произведем сжатие окружности к оси с коэффициентом , по формулам X = X¢,. Получим эллипс 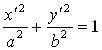c полуосями A, B. Таким образом, эллипс является образом окружности при преобразовании сжатия. 

Упражнение 1. Докажите, что любой эллипс является проекцией окружности X2 + Y2 = A2, находящейся в плоскости a на плоскость b, которая образует с угол j, cos j = B/A.

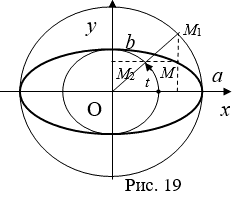
Выведем параметрические уравнения эллипса. Рассмотрим две концентрические окружности с центром в начале координат, радиусов A и B. Рассмотрим произвольный луч, выходящий из точки О и пересекающий данные окружности соответственно в точках M1 и M2. Пусть луч образует угол T с осью OX. Тогда точки M1 и M2 имеют координаты M1(A×cos T, A×Sin T) и M2(B×cos T, B×Sin T). Проведем через точку M1 прямую параллельную оси OY, через M2 прямую параллельную оси OY. Эти прямые пересекаются в точке M(A×cos T, B×Sin T). Покажем, что точка M лежит на эллипсе 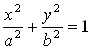. Действительно, имеем

.

Теперь, чтобы доказать, что уравнения

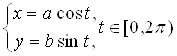(2)

Являются Параметрическими уравнениями эллипса достаточно показать, что координаты любой точки M(X1,Y1) эллипса находятся по формулам (1). Так как 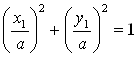, то найдется такое T€[0,2p), что Поэтому X1 = A×cos T, Y1 B×Sin T.

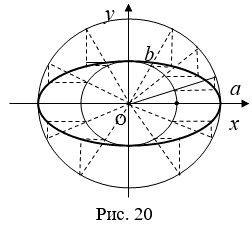
Замечание 1. Рассуждения, проведенные при выводе параметрических уравнений эллипса, дают способ построения сколь угодно много точек эллипса (см. рис. 20).

Определение 1. Эксцентриситетом e эллипса называется число, равное отношению его фокального расстоянию С к длине его большей полуоси A: .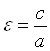

Из определения эллипса следует, что 0 £ e < 1. Для окружности эксцентриситет равен нулю.

Так как , то 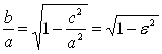. Из этого соотношения получаем, что чем ближе e к 1, тем меньше отношение B/A, при одинаковых значениях A тем более продолговатый эллипс.

< Предыдущая		Следующая >