65. Исследование эллипса по каноническому уравнению. Эллипса и окружность. Эксцентриситет эллипса. Параметрические уравнения эллипса

В § 1 доказано, что в канонической системе координат OXy Уравнение эллипса имеет вид:

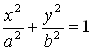. (1)

1. Эллипс не проходит через начало системы координат, так как координаты точки О(0,0) не удовлетворяют уравнению (1).

2. Найдем точки пересечения эллипса с осями координат. Для нахождения точки пересечения с осью ОХ полагаем в уравнении (1) У = 0 и находим X = ±A. Таким образом эллипс пересекает ось ОХ В точках A1(-A, 0), A2(A, 0). Аналогично находим, что эллипс пересекает ось ОY В точках B1(0,-B), B2(0, B).

Точки A1, A2, B1, B2 называются Вершинами эллипса, Отрезки A1A2, B1B2 Осями эллипса; |A1A2| =2A, |B1B2| =2B; числа A, B называются Полуосями эллипса. Так как A > B, То A1A2 называется Большой осью, B1B2 - Малой осью.

3. Так как все переменные входят в уравнение (1) в четной степени, то вместе с точкой (X, Y) эллипсу принадлежат четыре точки (±X, ±Y) (с произвольными комбинациями знаков). Таким образом, эллипс симметричен относительно, всех координатных осей OX, OY и начала координат. Точка О называется Центром эллипса.

4. Из уравнения эллипса находим, . Отсюда следует, что эллипс ограниченная линия, которая находится в прямоугольнике: -A £ X £ A, -B £ Y £ B (см. рис. 18).

5. Исследуем поведение эллипса в первой четверти. Для этого выразим Y из уравнения (1) через X:

.

Отсюда видим, в первой четверти на отрезке [0, A] эллипс является графиком убывающей функции.

6. Любая прямая, проходящая через начало координат, пересекает эллипс в двух точках. Действительно, вертикальная прямая, ось OY, пересекает эллипс в двух вершинах, любую другую прямую можно задать уравнением Y = Kx, K € R. Подставляя в уравнение (1) находим, что прямая пересекает эллипс в точках , где

< Предыдущая		Следующая >