54. Цилиндрическая система координат

Цилиндрическая система координат в пространстве задается точкой O, которая называется Началом цилиндрической системы координат, лучом L, выходящим из точки O, и вектором N единичной

длины, перпендикулярным L. Через точку O проведем плоскость a, перпендикулярную вектору N.

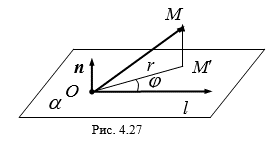
Пусть дана точка M. Опустим из ее перпендикуляр MM ¢ на плоскость a. Тогда цилиндрические координаты (R,J,H) Точки M определяются следующим образом: R, J - полярные координаты точки M ¢ на плоскости a по отношению полюсу O и полярной оси L, H - проекция вектора на вектор N. Координата R меняется на промежутке [0, +¥), координата J - На промежутке [0,2p) или на (-p, p], координата H - на промежутке (-¥, +¥).

Рассмотрим правую прямоугольную систему координат Oxyz c началом в точке O, ось Ox Направлена по оси L, направление оси Oz совпадает с направлением вектора N (cм. рис. 4.28).

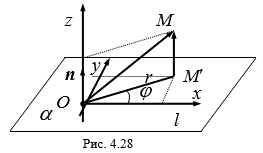
Пусть (R, J, H) - цилиндрические координаты точки A, (X, Y, Z) - прямоугольные координаты точки A. Как и в предыдущем параграфе находим формулы:

, , Z = H (7.1)

Из формул (7.1) находим

, H = Z, , (7.2)

Которые выражают цилиндрические координаты R, J, H Точки A через ее прямоугольные координаты X, Y, Z.

< Предыдущая		Следующая >