52. Основные задачи, решаемые в прямоугольной системе координат

В прямоугольной системе координат решаются все те задачи, которые решаются в аффинной системе координат, а решаются так называемые Метрические задачи, связанные с измерением отрезков, углов, площадей и объемов.

1. Измерение длины отрезка. Найти расстояние между точками

A(X1, Y1, Z1), B(X2, Y2, Z2) в прямоугольной системе координат Oxyz. Расстояние меду точками и равно длине вектора

= (X2 - X1, Y2 - Y1, Z2 - Z1). (5.1)

По формуле для длины вектора находим

. (5.2)

Для точек A(X1, Y1), B(X2, Y2) плоскости Oxy формула (5.2) принимает вид

, (5.3)

А для точек A(X1), B(X2) прямой Ox -

. (5.4)

2. Измерение углов. Угол A В треугольнике ABC равен углу между векторами A = и B = .

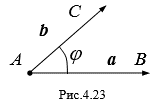
Угол j между ненулевыми векторами A = (X1, Y1, Z1), B = (X2, Y2, Z2) легко находится из определения скалярного произведения векторов Ab = |A||B|cos j и формулы для скалярного произведения векторов в координатной форме:

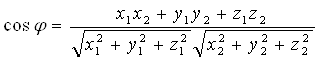. (5.5)

Для векторов плоскости формула (5.5) принимает вид:

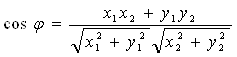. (5.6)

Из формулы для определения модуля векторного произведения векторов легко найти формулу для синуса угла между векторами A И B.

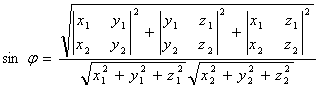. (5.7)

Для случая пространства углы между векторами неориентированные и не имеют знака. Для случая плоскости углы между векторами ориентированные и имеют знак. Угол Ð( A, B) называется Положительным, если поворот от вектора к по наименьшему углу совершается против часовой стрелки, и Отрицательным в противном случае.

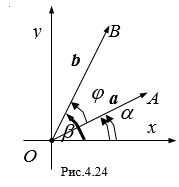
По определению косинуса и синуса произвольного угла имеем

.

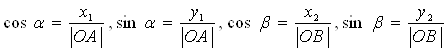Так как j = b - a, , то получаем

.

Последнюю формулу можно записать в виде

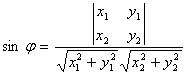. (5.8)

Из формул (5.6) и (5.8) получаем формулу для тангенса угла между векторами

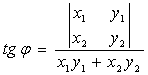. (5.9)

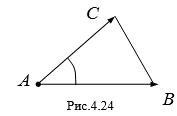
3. Измерение площадей. Любой многоугольник можно диагоналями разбить на треугольники, поэтому вычисление площади любого многоугольника сводится к вычислению площади треугольника. Вычислим площадь треугольника ABC, у которого заданы координаты вершин A(X1, Y1, Z1), B(X2, Y2, Z2) , С(X3, Y3, Z3) в прямоугольной системе координат Oxyz. Рассмотрим векторы = (X2 - x1, Y2 - Y1, Z2 - Z1), = (X3 - x1, Y3 - Y1, Z3 - Z1). По определению векторного произведения векторов площадь S треугольника ABC, вычисляется по формуле . Тогда получаем

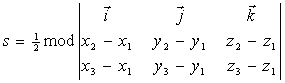. (5.10)

Отсюда находим

.

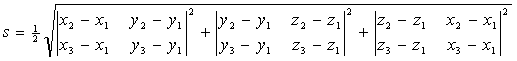Площадь плоского треугольника ABC, у которого заданы координаты вершин A(X1, Y1), B(X2, Y2) , С(X3, Y3) в прямоугольной системе координат Oxy Можно найти, используя формулу синуса угла между векторами

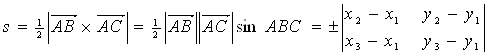, (5.11)

Где стоит знак "+", если поворот от вектора к вектору по наименьшему углу осуществляется против часовой стрелки, т. е. обход треугольника ABC осуществляется против часовой стрелки, знак "-" - в противном случае. В первом случае говорят, что треугольник ориентирован Положительно, а во втором - Отрицательно.

4. Измерение объемов. Любой многогранник можно плоскостями разбить на треугольные пирамиды, поэтому вычисление объема любого многогранника сводится к вычислению объема треугольной пирамиды. Вычислим объем треугольной пирамиды ABCD, у которой заданы координаты вершин A(X1, Y1, Z1), B(X2, Y2, Z2) , С(X3, Y3, Z3), , С(X4, Y4, Z4) в прямоугольной системе координат Oxyz. Рассмотрим векторы = (X2 - x1, Y2 - Y1, Z2 - Z1), = (X3 - x1, Y3 - Y1, Z3 - Z1) , = (X4 - x1, Y4 - Y1, Z4 - Z1). По свойству смешенного произведения векторов модуль смешенного произведения векторов площадь объему параллелепипеда, построенного на этих векторах. Отсюда объем V треугольной пирамиды ABCD, вычисляется по формуле . Тогда получаем

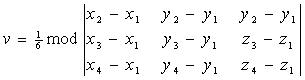. (5.12)

< Предыдущая		Следующая >