51. Формулы преобразования прямоугольной системы координат

Для прямоугольной системы координат имеют место все формулы, имеющие место для произвольной аффинной системы координат.

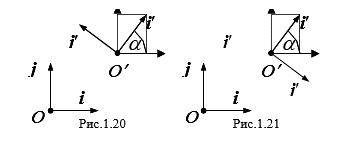
Рассмотрим случай преобразования прямоугольных систем координат на плоскости. Пусть на плоскости даны две прямоугольные системы координат (О, I, J) и (О¢, I¢, J¢). Пусть точка О¢ в системе (О, I, J) имеет координаты O¢(X0, Y0), а T = (Tij) матрица перехода от базиса старой системы координат к базису новой. Пусть точка A имеет в старой и соответственно в новой системах координат координаты A(X,Y) и A(X¢,Y¢). По формуле (3.4) имеем

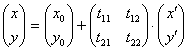. (4.1)

Чтобы применить эти формулы, разложим вектора I¢, J¢ по векторам I, J. Для этого обозначим через a угол между векторами I, I¢. Отсюда получим

I¢= cos a ×I +sin a× J,

J¢= cos (a ± p/2)× I +sin (a ± p/2)× J = - e×sin a× I +e×cos a × J,

Где число e, равно 1 или -1 в соответствии с тем базисы I, J и I¢, J¢¢ ориентированны одинаково или противоположно (см. рис. 4.20, 4.21). Тогда получим матрицу перехода от первого базиса ко второму, а из формулы (4.1) следуют формулы преобразования прямоугольных координат плоскости

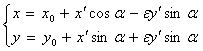, (4.2)

Где число e, равно 1 или -1 в соответствии с тем новая и старая системы координат ориентированны одинаково или противоположно.

Если начала и ориентации старой и новой систем координат совпадают, то одна система получается из другой поворотом на угол a. В этом случае формулы (4.2) принимают вид

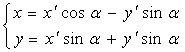. (4.3)

И называются Формулами поворота прямоугольной системы координат.

< Предыдущая		Следующая >