49. Формулы преобразования аффинной систем координат

1. Пространства. Пусть в пространстве даны две аффинные системы координат (О, V1, V2, V3) и (О¢, V1¢, V2¢, V3¢), первую систему координат называем Старой, а вторую Новой.

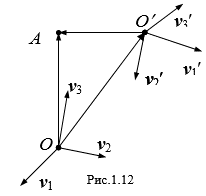
Пусть точка О¢ в системе (О, V1, V2, V3) имеет координаты O¢(X0, Y0, Z0), а T = (Tij) матрица перехода от базиса старой системы координат к базису новой. Пусть точка A имеет в старой и новой системах координат соответственно координаты A(X,Y,Z) и A(X¢,Y¢,Z¢). По определению координат точки имеем,

=XV1 + YV2 + ZV3, = X¢V1¢+ Y¢V2¢ + Z¢V3¢, =X0V1 + Y0V2 + Z0V3.

По определению матрицы перехода от одного базиса к другому имеем:

V1¢ = T11V1 + T21V2 + T31V3, V2¢ = T12V1 + T22V2 + T32V3, V3¢ = T13V1 + T23V2 + T33V3.

Так как , то получаем другое представление вектора

= (X0V1 + Y0V2 + Z0V3) + (X¢V1¢+ Y¢V2¢ + Z¢V3¢) =

= (X0V1 + Y0V2 + Z0V3) + X¢(T11V1 + T21V2 + T31V3) + Y¢(T12V1 + T22V2 + T32V3) + Z¢(T13V1 + T23V2 + T33V3) =

= (X0 + X¢T12 + Y¢T12 + Z¢T13)V1 + (Y0 + X¢T22 + Y¢T22 + Z¢T23)V2 + + (Z0 + X¢T32 + Y¢T32 + Z¢T33)V3.

В силу единственности представления вектора через векторы базиса получаем формулы

X = x0 + T12X¢ + T12Y¢ + T13Z¢,

Y = y0 + T22X¢ + T22Y¢ + T23Z¢, (3.1)

Z = Z0 + T22X¢ + T22Y¢ + T23Z¢,

Которые называются Формулами преобразования координат точки при переходе от одной системы координат к другой. Формулы (3.1) удобно записать в матричной форме:

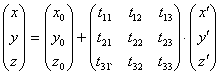. (3.2)

2. Плоскости. Пусть на плоскости даны две аффинные системы координат (О, V1, V2) и (О¢, V1¢, V2¢), (Старая и Новая). Пусть точка О¢ в системе (О, V1, V2) имеет координаты O¢(X0, Y0), а T = (Tij) матрица перехода от базиса старой системы координат к базису новой. Пусть точка A имеет в старой и новой системах координат соответственно координаты A(X,Y) и A(X¢,Y¢). Повторяя рассуждения предыдущего пункта, получим следующие формулы преобразования координат плоскости:

X = x0 + T11X¢ + T12Y¢, Y = y0 + T22X¢ + T22Y¢, (3.3)

Которые удобно записать в матричной форме:

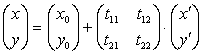. (3.4)

3. Прямой. Пусть на прямой даны две аффинные системы координат (О, V1) и (О¢, V1¢), (старая и новая). Пусть точка О¢ в системе (О, V1) имеет координаты O¢(X0), а T = (T11) матрица перехода от базиса старой системы координат к базису новой. Пусть точка A имеет в старой и новой системах координат соответственно координаты A(X) и A(X¢). Повторяя рассуждения предыдущего пункта, получим следующие формулы преобразования координат плоскости:

X = X0 + T11X¢. (3.5)

4. Параллельного переноса. Осуществим параллельный перенос системы координат (О, V1, V2, V3), так, чтобы ее новое начало оказалось в точке O¢(X0, Y0, Z0). Получим новую систему координат (О¢, V1, V2, V3). Матрица T = (Tij) перехода от базиса V1, V2, V3 к базису V1, V2, V3 является единичной матрицей и формулы (2.1) принимают вид:

X = x0 + X¢,

Y = Y0 + Y¢, (3.6)

Z = Z0 + Z¢,

Которые называются Формулами параллельного переноса.В случае плоскости они принимают следующий вид,

X = X0 + X¢, Y = Y0 + Y¢, (3.7)

В случае прямой -

X = x0 + X¢.

< Предыдущая		Следующая >