45. Смешенное произведение векторов в координатной форме

Пусть I, J, K ортонормированный базис пространства V3, вектора которого образуют правую тройку. Пусть A = (X1, Y1, Z1), B = (X2, Y2, Z2) , С = (X3, Y3, Z3) координаты этих векторов в базисе I, J, K. Тогда по формулам (5) § 5 и (1) § 6 получим

A´B =( 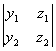, -,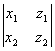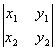), (A´B)C = 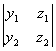X3 - Y3 + Z3.

Последнюю формулу по теореме о разложения определителя по строке можно записать в виде:

(A´B)C =. (2)

Так как при перестановке двух строк в определителе значение определителя меняется на противоположное, то при перестановке двух векторов в смешенном произведении его знак меняется на противоположный:

Abc = -Bac = Bca = -Bac = Cab = -Cba. (3)

Из теоремы 1 получаем следствие.

Следствие 1. Пусть A = (X1, Y1, Z1), B = (X2, Y2, Z2) , С = (X3, Y3, Z3) Координаты векторов в ортонормированном базисе. Тогда объем V параллелепипеда, построенного на этих векторах равен модулю определителя, составленного из координат этих векторов:

V = |(A´B)C| =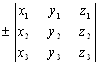, (4)

Где стоит знак "+", если Тройка векторов A, B, C правая, знак "-", Если тройка векторов A, B, C - левая.

Следствие 2. Векторы A = (X1, Y1, Z1), B = (X2, Y2, Z2) , С = (X3, Y3, Z3) Компланарны тогда и только тогда, когда определитель, составленный из координат этих векторов равен нулю, т. е.

=0.

< Предыдущая		Следующая >