44. Смешенное произведение

1. Определение смешенного произведения и его свойства.

Определение 1. Смешенным произведением трех векторов A, B, C Называется скалярное произведение векторного произведения векторов A и B На вектор C. Смешенное произведение векторов A, B, C обозначается символом Abc. Таким образом, по определению

Abc = (A´B)C.

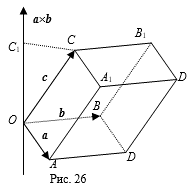
Теорема 1. Модуль смешенного произведения трех некомпланарных векторов A, B, C равен объему параллелепипеда, построенного на этих векторах, при этом, если тройка векторов A, B, C правая, то Abc > 0, если тройка векторов A, B, C - левая, то Abc < 0.

Доказательство. Отложим векторы A, B, C от точки O: A = , B = , C = , и построим на их как на ребрах параллелепипед OADBCA1D1B1 . Через точку О проведем прямую L перпендикулярную плоскости OAB. Найдем проекцию С1 точки С на прямую L. Тогда вектор является проекцией вектора на L. Длина вектора равна высоте H построенного параллелепипеда.

Построим вектор A´B, который по определению ортогонален векторам A И B, и поэтому перпендикулярен плоскости OAB. Таким образом, вектор A´B коллинеарен вектору . По свойству скалярного произведения

(A´B) C = |A´B| прA´B C = ±|A´B||| = ± SОснов.× h = ±V параллелепипеда, (1)

Где стоит знак "+", если A´B , и стоит знак "-", если A´B ¯. Таким образом, |(A´B) C| = V параллелепипеда.

Далее A´B Тогда и только тогда, когда тройки векторов A, B, A´B и A, B, C ориентированы одинаково, т. е. A, B, C правая тройка. Тогда из (1) следует, что, если тройка векторов A, B, C Правая, то Abc > 0, Если тройка векторов A, B, C - Левая, то Abc < 0.

Теорема 2. Векторы A, B, C компланарны тогда и только тогда, смешенное произведение Abc = 0.

Доказательство. (Þ) Пусть векторы A, B, C компланарны. Вектор A´B ортогонален векторам A и B, и поэтому он ортогонален вектору C, который изображается в плоскости, параллельной векторам A и B. Так как A´B^C, то (A´B)C = 0.

(Ü) Пусть Abc = 0. Докажем, что векторы A, B, C компланарны. Если допустить, что они некомпланарны, то объем V параллелепипеда, построенного на этих векторах ≠ 0. Тогда по теореме 1 Abc = =±V ≠ 0. Получаем противоречие.

< Предыдущая		Следующая >