43. Векторное произведение векторов в координатной форме

Пусть I, J, K ортонормированный базис пространства V3, вектора которого образуют правую тройку. Пусть A = (X1, Y1, Z1), B = (X2, Y2, Z2) координаты этих векторов в базисе I, J, K. Тогда имеем

A = X1I + Y1J + Z1K, B = X2I + Y2J + Z2K.

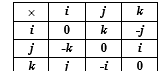
Так как базис ортонормированный, и его вектора образуют правую тройку, то имеем следующую таблицу умножения базисных элементов I, J, K. Тогда по свойствам векторного произведения находим:

A´B = (X1I + Y1J + Z1K)´(X2I + Y2J + Z2K) =

=(X1X2)(I´I) + (X1Y2)(I´J) + +(X1Z2)(I´K) + (Y1X2)(J´I) + (Y1Y2)(J´J) + (Y1Z2)(J´K) + (Z1X2)(K´I) + (Z1Y2)(K´J) + (Z1Z2)(K´K) =

= (Y1Z2 - Z1Y2)I - (Z1X2 -X1Z2)J + (X1Y2 - Y1X2) K .

Таким образом, получаем следующую формулу для вычисления векторного произведения векторов в ортонормированном базисе:

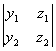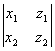A´B = I - J +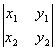K , (1)

Которую можно записать в виде определителя

A´B = 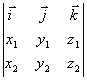. (2)

В силу сделанного выше замечания площадь S параллелограмма, построенного на неколлинеарных векторах A = (X1, Y1, Z1), B = (X2, Y2, Z2), заданных своими координатами в ортонормированном базисе вычисляется по формуле:

S = |A´B|= 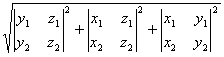. (3)

< Предыдущая		Следующая >