42. Векторное произведение
1. Ориентация векторов. В пространстве различают два вида упорядоченных троек векторов.
Определение 1. Упорядоченная тройка некомпланарных векторов A, B, C Называется Правой (Левой), если эти вектора, отложенные от одного начала, располагаются так же, как расположены большой, указательный средний пальцы правой (левой) руки.
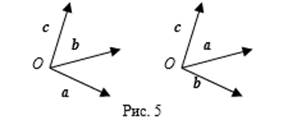
Данному правило различия правой и левой троек векторов можно придать следующие равносильные формулировки.
Правило правого винта или буравчика. Упорядоченная тройка некомпланарных векторов A, B, C Является Правой (Левой), если правый (левый) винт вращать по наименьшему углу от вектора A к B, то направление винта совпадает с направлением вектора C.
Тройка A, B, C правая, если смотреть с конца вектора на плоскость векторов, то поворот A от B к по кратчайшему углу происходит против часовой стрелки.
Замечание 1. Так как в самой геометрии нет понятия правого и левого, то необходимо дать такое определение, которое основывается только на понятиях самой математики. Для этого выберем, какую-нибудь тройку векторов и назовем ее основной (правой). Далее две тройки векторов назовем Ориентированными одинаково (Противоположно), если определитель матрицы перехода от первой тройки ко второй >0 (<0). Тогда все тройки, ориентированные одинаково с основной тройкой назовем правыми, а остальные тройки назовем левыми.
2. Векторное произведение.
Определение 7. Векторным произведением неколлинеарных векторов A и B называется вектор С, который обладает следующими свойствам:
1) длина вектора С равна произведение модулей этих векторов на синус угла между этими векторами, т. е. |С| = |A||B| sin Ð( a, B);
2) вектор С ортогонален векторам A и B;
3) векторы A, B, с образуют правую тройку векторов.

Векторное произведение векторов A и B обозначается символом
A ´ B или [A, B].
Из определения 7 следует, что модуль векторного произведения неколлинеарных векторов равен площади параллелограмма, построенного на этих векторах. Если векторов A, B коллинеарны, то полагаем векторное произведение равным 0.
Теорема 1. Для любых векторов A, B, C и для любого числа L справедливы следующие свойства:
1) A ´ a = 0,
2) A ´ b = -B ´ A - антикоммутативный закон,
3) (l A) ´ B = l (A ´ B) - ассоциативный закон,
4) (A + B) ´ C = A ´ C + B ´ C - дистрибутивный закон.
Доказательство. 1. Так как Ð( a, A) = 0, то | a ´ a| = |A||A| sin 0 = 0, и A ´ a = 0.
2. По первому свойству определения 7 модули векторов A ´ b, B ´ A равны. По второму свойству - эти вектора ортогональны векторам A и B и поэтому коллинеарны. По третьему свойству они противоположно направлены. Отсюда следует, что A ´ b = -B ´ A.
3. По первому свойству определения 7, и определению произведения вектора на число модули векторов (l A) ´ B, l (A ´ B) равны |l| |A||B| sinÐ( A, B). По второму свойству - эти вектора коллинеарны. Если l> 0, они сонаправлены с вектором A ´ b, Если l < 0, они направлены противоположно вектору A ´ b. Отсюда следует равенство 2.
4. Если хотя бы один из векторов A, B, C Равен 0 То свойство 4 очевидно. Допустим, что эти вектора неравны нулю, и отложим их от точки O: A = ![]() , B =
, B = ![]() , C =
, C = ![]() , и проведем через точку плоскость a перпендикулярную направленному отрезку
, и проведем через точку плоскость a перпендикулярную направленному отрезку ![]() (см. рис. 25).
(см. рис. 25).
Если вектор A неколлинеарен вектору C, то вектор A ´ C ортогонален векторам A И C И поэтому лежит в плоскости a. Спроектируем точку A на плоскость a. Получим вектор отрезок ![]() , длина которого равна |A| sinÐ( A, С). Вектор A ´ C ортогонален вектору
, длина которого равна |A| sinÐ( A, С). Вектор A ´ C ортогонален вектору ![]() , его длина равна |A||С| sin Ð( a, С) =
, его длина равна |A||С| sin Ð( a, С) = ![]() |С|. Тройка векторов A, C, A ´ C - правая.
|С|. Тройка векторов A, C, A ´ C - правая.
Таким образом, A ´ C получается из вектора A По правилам:
Спроектируем ![]() на плоскость, получим вектор
на плоскость, получим вектор ![]() ;
;
Повернуть вектор ![]() На плоскости на угол 90 по правилу правой руки, получим вектор
На плоскости на угол 90 по правилу правой руки, получим вектор ![]() ;
;
Умножим вектор ![]() на число |С|.
на число |С|.
Очевидно, это справедливо и в том случае, когда векторы A и C коллинеарен.
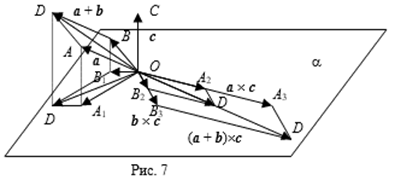
Аналогичным образом получатся векторы (A + B) ´ C и B ´ C из векторов A + B и B (см. рис. 25).
Имеем A + B =![]() =
= ![]() +
+![]() , то по свойству проекции имеем
, то по свойству проекции имеем ![]() =
=![]() +
+![]() . Повернем каждый из векторов
. Повернем каждый из векторов ![]() ,
,![]() ,
,![]() на угол 90о, если смотреть на плоскость a с конца вектора C. Получим вектора
на угол 90о, если смотреть на плоскость a с конца вектора C. Получим вектора ![]() ,
,![]() ,
,![]() . Так как при повороте взаимное расположение векторов сохраняется, и сумма векторов переходит в сумму векторов, то
. Так как при повороте взаимное расположение векторов сохраняется, и сумма векторов переходит в сумму векторов, то ![]() =
=![]() +
+![]()
Умножением каждый из векторов ![]() ,
,![]() ,
,![]() на число |A| и получим вектора
на число |A| и получим вектора ![]() ,
,![]() ,
,![]() , равные соответственно векторам (A + B) ´ C, A ´ C, B ´ C. В силу дистрибутивного закона
, равные соответственно векторам (A + B) ´ C, A ´ C, B ´ C. В силу дистрибутивного закона ![]() =|A|
=|A|![]() =|A|
=|A|![]() +|A|
+|A|![]() =
= ![]() +
+![]() . Поэтому (A + B) ´ C = A ´ C + B ´ C.
. Поэтому (A + B) ´ C = A ´ C + B ´ C.
| < Предыдущая | Следующая > |
|---|