36. Скалярное произведение. Угол между векторами

1. Числовая ось. Прямая L, на которой выбрано начало отсчета - точка O, положительное направление и единичный отрезок, называется Числовой осью. Числовую ось можно также задать точкой O и вектором E единичной длины, параллельным оси. Вектор E Называется Ортом числовой оси. В качестве единичного отрезка выбирается конец вектора = E, отложенного от точки O.

Координатой точки A на числовой оси называется координата X вектора в базисе E: = X E. Координату точки обозначаем символом A(X). Координаты точки устанавливают биективное соответствие между множеством всех точек прямой и множеством R действительных чисел.

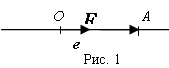
2. Угол между векторами.

Определение 1. Углом J Между векторами A, B называется угол между направленными отрезками , , которыми изображаются данные вектора и которые отложены из одной точки.

Угол между векторами обозначаем символом Ð(A, B).

Если вектора A, B коллинеарны, то угол между векторами считается равным нулю. Если хотя бы один из векторов A или B нулевой, угол между векторами A и B неопределен.

Угол меду векторами в пространстве не ориентированный. Угол меду векторами на плоскости ориентированный. Угол считается положительным, если поворот от первого вектора ко второму совершается в направлении против часовой стрелки. В противном случае угол считается отрицательным.

Нетрудно доказать, что угол меду векторами не зависит от точки O.

< Предыдущая		Следующая >