35. Базис векторов пространства

Рассмотрим множество V3 всех векторов пространства.

Теорема 5. Любая упорядоченная система трех некомпланарных векторов A, B, С € V3 Образуют базис векторного пространства V3.

Доказательство. Пусть A, B, С Некомпланарные векторы. По следствию 1 теоремы 8 они образует линейно независимую систему. Пусть D € V3. Отложим векторы A, B, С и D от точки O: A = , B = , С = , D = (см. рис. 18). Проведем через точку D прямую L, параллельную прямой OD. Так как векторы A, B, С некомпланарны, то прямая L пересекает плоскость OAB в точке E. Тогда =+. Так как векторы лежит в плоскости OAB, а вектора образуют базис векторов этой плоскости, то по теореме 7 = a a + b b, где a, b € R. Так как вектор коллинеарен вектору C, То по теореме 8 § 1 он линейно выражается через вектор С: = g с. Поэтому D = = a a + b b + g с и по определению 1 вектора A, B, С образует базис пространства V3.

По теореме 5 базис векторов на пространстве образуют любые три некомпланарные вектора, поэтому любой вектор в пространстве имеет три координаты. Тогда справедливо следующее утверждение.

Следствие 1. Вектора A = (a1, b1, g1), B = (a2, b2, g2), С = (a3, b3, g3) Образуют базис векторов пространства тогда и только тогда, когда

= 0.

Теорема 6. Любые четыре вектора A, B, С, D В пространстве линейно зависимы.

Доказательство. Если векторы A, B, С Компланарны, то по теоремы 5 они линейно зависимы. Тогда по свойству линейной зависимости по свойству 4 § 3 вектора A, B, С, D линейно зависимы. Если вектора A, B, С некомпланарны, то по теореме 5 они образуют базис векторов пространства. Тогда вектор D линейная комбинация векторов A, B, С и по свойству линейной зависимости векторы A, B, С, D линейно зависимы.

Задача 1. Доказать что векторы A = (1, 2, 0), B = (3, 2, 1), С = (0, 1, -1) образуют базис в пространстве и выразить вектор D = (5, 5, 2) через векторы базиса.

Решение. Так как определитель

,

То векторы A, B, С образуют базис пространства V3.

Для того, чтобы найти координаты вектора D в базисе A, B, С составим векторное уравнение

X A + Y B + Z C = 0. (14)

И запишем его в координатной форме:

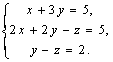
Решаем эту систему линейных уравнений: X = 2, Y = 2, Z = -1 и находим D = 2A + B - С.

< Предыдущая		Следующая >