34. Базис векторов на плоскости

Множество V2 векторов фиксированной плоскости образует векторное пространство.

Теорема 3. Любая упорядоченная система двух неколлинеарных векторов A, B € V2 образуют базис векторного пространства V2.

Доказательство. Пусть A и B неколлинеарные вектора плоскости. По следствию 2 теоремы 2 векторы A и B образует линейно независимую систему. Пусть С € V2. Отложим векторы A, B и С от точки O: A = , B = И С = (см. рис. 17). Проведем через точку C прямую L, параллельную прямой OB. Так как векторы A и B неколлинеарны, то прямые OA И L пересекаются в точке D. Тогда =+. Так как векторы И Соответственно коллинеарны векторам A и B, то по свойству линейной зависимости они соответственно линейно выражается через векторы A и B: =a a, =b b. Поэтому с = = a a + b b, и по определению 1 вектора A и B образует базис пространства V2.

По теореме 3 базис векторов на плоскости образуют любые два неколлинеарные вектора, поэтому любой вектор на плоскости имеет две координаты. Тогда справедливо следующее утверждение.

Следствие 1. Вектора A = (a1, b1), B = (a2, b2) Образуют базис векторов плоскости тогда и только тогда, когда

= 0.

Теорема 4. Векторы A, B и С Компланарны тогда только тогда, когда они линейно зависимы.

Доказательство. Пусть вектора A, B и С Компланарны. По определению они могут быть изображены на одной плоскости p. Если вектора A, B коллинеарны, то по следствию 1 теоремы 2 они линейно зависимы.

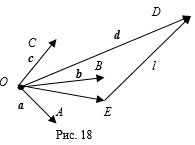
Тогда по свойству по свойству линейной зависимости вектора A, B, С линейно зависимы. Если вектора A, B неколлинеарны, то по теореме 3 они образуют базис векторов плоскости p. Тогда вектор С линейная комбинация векторов A, B, и по свойству линейной зависимости векторы A, B, С линейно зависимы.

Обратно, если векторы A, B, С линейно зависимы, то по свойству линейной зависимости, один из этих векторов линейно выражается через два другие. Тогда вектора могут быть изображены одной плоскости и поэтому Коллинеарны.

Следствие 1. Векторы A, B и С Некомпланарны тогда только тогда, когда они линейно независимы.

< Предыдущая		Следующая >