37. Векторная проекция вектора на прямую
Определение 2. Проекцией точки A на прямую L Называется основание A¢ перпендикуляра AA¢, опущенного из точки A на прямую L.
Определение 3. Проекцией направленного отрезка ![]() На прямую L Называется направленный отрезок
На прямую L Называется направленный отрезок ![]() , где A¢ и B¢ Соответственно проекции точек A и B На прямую L.
, где A¢ и B¢ Соответственно проекции точек A и B На прямую L.
Определение 4. Проекцией (Векторной проекцией) Вектора A на прямую L Называется вектор, изображаемый проекцией направленного отрезок, который изображает данный вектор a.
Векторная проекция вектора A на прямую L изображается символом ПрL A.
Теорема 1. Векторная проекция ПрL A не зависит от направленного отрезка, которым изображается данный вектор a.
Доказательство. Пусть вектор A изображается направленным отрезком ![]() ,
, ![]() Проекция
Проекция ![]() на прямую L (см. рис. 21).
на прямую L (см. рис. 21).
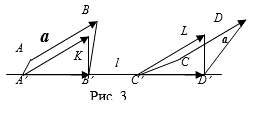
Точки A¢ и B¢ можно получить, проведя через точки A и B плоскости перпендикулярные прямой L. От точки A¢ отложим вектор A: a =![]() . Четырехугольник A¢ABK - прямоугольник. Так как A¢A ^ L, То BK ^ L и плоскость B¢BK ^ L. Тогда BK ^ L и точка B¢ - Проекция точки K. Таким образом, направленные отрезки
. Четырехугольник A¢ABK - прямоугольник. Так как A¢A ^ L, То BK ^ L и плоскость B¢BK ^ L. Тогда BK ^ L и точка B¢ - Проекция точки K. Таким образом, направленные отрезки ![]() и
и ![]() имеют одну и туже проекцию
имеют одну и туже проекцию![]() .
.
Пусть вектор A изображается также направленным отрезком ![]() ,
, ![]() проекция
проекция ![]() на прямую L. От точки С¢ отложим вектор A: a =
на прямую L. От точки С¢ отложим вектор A: a =![]() . Направленные отрезки
. Направленные отрезки ![]() и
и ![]() имеют одну и туже проекцию
имеют одну и туже проекцию ![]() . Докажем, что
. Докажем, что ![]() =
=![]() .
.
Так как треугольники A¢B¢K И C¢D¢L равны, то A¢B¢ = C¢D¢. Так как лучи A¢ B¢ И C¢ D¢ Сонаправлены, то ![]() =
=![]() .
.
Теорема 2. Для любой прямой L, Для Любых векторов A, B и для любого числа L справедливы следующие свойства:
1) ПрL (A + B) = ПрL A + ПрL B;
2) ПрL (l A) = l ПрL A.
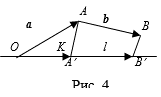
Доказательство. Возьмем точку O на прямой L И построим сумму векторов a, B: A + B =![]() =
= ![]() (см. рис. 22). Пусть A¢ И B¢ проекции точек A И B на прямую L. Тогда
(см. рис. 22). Пусть A¢ И B¢ проекции точек A И B на прямую L. Тогда
ПрL (A + B) =![]() =
=
= ПрL A + ПрL B.
Свойство 2 докажите самостоятельно ( рассмотрите три случая l =0, l > 0, l < 0).
| < Предыдущая | Следующая > |
|---|