31. Вычитание векторов
Определение 12. Разностью Двух векторов A и B, называются такой третий вектор С, обозначаемый символом A - B, при сложении которого с вектором B получаем вектор A.
Теорема 7. Для любых векторов A, B Разность A - B существует, единственна и вычисляется по формуле:
A - B = A + (-B). (1)
Доказательство. Так как
(A + (-B)) + B = A + ((-B) + B) = A + 0 = A,
То вектор A + (-B) разность векторов A и B. Доказывая единственность разности допустим, что векторы С и D являются разностью векторов A и B. Тогда по определению разности имеем B + С = A И B +D = A. Отсюда B + С = B +D. Прибавляя к обеим частям этот равенства вектор получаем (-B) + (B + С) = (-B)+ (B +D). Применяя свойства теоремы 6 последовательно получаем равенства:
((-B) + B) + С) = ( (-B)+ B) +D,
0 + С = 0 +D,
С = D.
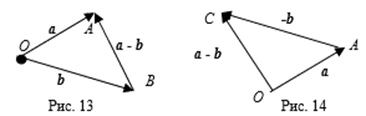
Разность векторов A И B геометрически можно найти двумя способами по определению 12 (см. рис. 13) и по теореме 7 (см. рис 14). По определению 12 разность A - B равна вектору, выходящему из конца второго вектора B в начало первого A, если векторы A И B отложены от одной точки. По теореме 7 разность A - B равна сумме векторов A + (-B).
| < Предыдущая | Следующая > |
|---|