32. Операция умножения вектора на число и ее свойства
Определение 13. Произведением вектора A на число L Называется такой вектор B, что
1) | B | = | L || A |
2) если l > 0, то AB, если l < 0, то A¯B, если l = 0 или A = 0, то B = 0.
Произведение вектора A на число l обозначается символом L A. Числа называют также Скалярными величинами или Скалярами.
Теорема 8. Вектора A ≠ 0 Коллинеарен вектору B тогда и только тогда, когда найдется такое число, что B = L A.
Доказательство. Если, то по определения 13 следует, что векторы коллинеарны. Обратно, пусть вектора коллинеарны. Тогда, полагая L = ±|B|/|A|, где стоит знак "+", если AB, стоит знак "-", если A¯B, по определению 13 получим B = L A.
Теорема 9. Для любых векторов A, B и для любых чисел l, m Справедливы свойства:
1) l(m A) = (lm) A - Смешенный ассоциативный закон;
2) (l + m) A = l A+ m A - Дистрибутивный закон;
3) l (A + B) = l A + l B - Дистрибутивный закон;
4) 1 A = A - Свойство умножения на единицу.
Доказательство. 1. Если векторы A или B равны 0 Или числа m равны нулю, то равенства 1-3 теоремы почти очевидны (проверте их). Также по определению равенства векторов проверяется равенство 4. Поэтому дальше будем считать, что A ≠ 0, B ≠ 0, lm ≠ 0.
1. Длины векторов l(m A), (lm) A равны |l||m| |A|, и поэтому равны между собой. Далее оба эти вектора коллинеарны вектору A. Если числа l и m одного знака, то направление векторов l(m A), (lm) A совпадает с направлением вектора A. Если числа l и m противоположных знаков, то эти векторы противоположны вектору A. Отсюда по определению векторы l(m A), (lm) A равны.
2. Если числа l и m одного знака, то векторы (l + m) A, l A, m A сонаправлены и |l A+m A| = |l A|+|m A|= |l ||A| + | m|| A| = (| l | + | m | )| A|.
Так как в этом случае |l + m | = | l | + | m |, то |(l + m) A| = || l A + m A|.
Отсюда, по определению равенства векторов (l + m) A = l A + m A.
Случай, когда числа l и m противоположного знака рассмотрите самостоятельно.
3. Если векторы A и B коллинеарны, то по теореме 8 его можно представить в виде B = m A. Тогда по свойствам 1, 2 и 4 имеем
L (A + B) = l (1A + m A) = l (1A) + l (m A) =l A + l (m A) = l A + l B.
Если векторы A и B неколлинеарны, то построим сумму A + B = ![]() =
= ![]() +
+![]() .
.
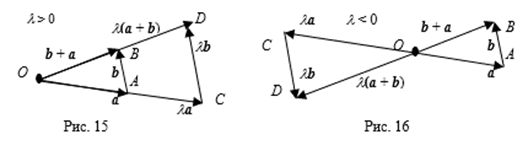
Построим вектор l A =![]() , l (A + B) =
, l (A + B) = ![]() (см. рис. 15 при l > 0 и рис. 16 при l < 0). Получим, что треугольники ОAB и OCD подобны. Из подобия треугольников и определения 13 получаем, что
(см. рис. 15 при l > 0 и рис. 16 при l < 0). Получим, что треугольники ОAB и OCD подобны. Из подобия треугольников и определения 13 получаем, что ![]() = l A. Отсюда находим, что l (A + B) =
= l A. Отсюда находим, что l (A + B) = ![]() = =
= =![]() +
+![]() =lA + l B.
=lA + l B.
Пространство геометрических векторов. Множество V3 всех геометрических векторов пространства является векторным пространством на полем действительных чисел относительно операций сложения векторов и умножения вектора на число (см. теоремы 6 и 9 § 1).. Также векторным пространством является множество V2 (V1) всех векторов плоскости (прямой).
Множество всех геометрических векторов, коллинеарных данному вектору A образует подпространство пространства V3 всех геометрических векторов.
| < Предыдущая | Следующая > |
|---|